What Selection Pressure Does to Mutations Favoring Cancer? Highlights of A Simulation Approach

What Selection Pressure Does to Mutations Favoring Cancer? Highlights of A Simulation Approach

Research Document

Context: research in oncogenetics has focused for years on mutations increasing independently the risk of cancer (ex. BRCA mutations for breast/ovarian cancers). Nowadays, interactions between mutated genes are searched for. Besides, because deleterious mutations shorten life and thus reproduction outcomes, why have they not been eliminated by selection pressure?

Methods: we developed software to test various hypotheses about mutations survival among a theoretical population having main demographic characteristics of a primitive population. Various simulations (Monte-Carlo approach) with various genotypes tested how several deleterious mutated genes with various penetrances could interact and possibly survive despite the life shortening they induce.

Results: simulation over millennia showed that deleterious mutations needed to provide evolutionary compensations such as higher fertility and/or earlier onset of reproductive capacities. This las characteristic was a strong factor enabling deleterious mutations to last. Because in female, menopause terminates the fertility period, iterations tended to select spontaneously mutations favoring cancer after menopause, without any consideration about hormonal exposure. Interactions between highly penetrant mutations were very unlikely to last and tended to split apart populations carrying each different mutation. Some results regarding fertility were validated using our database of 9000 pedigrees at high cancer risk.

Introduction

Very penetrant germline (hereditary) mutations in Human are scarce [1] and reports of de novo mutations are quite rare [2,3]. Even if this statistic is not exactly right, this means that mutations favoring cancer like BRCA1 and BRCA2 are very uncommon events in human's history and it is very likely that present known mutations are quite old (several millennia). Other etiologic hypotheses concerning hereditary cancer risk suggest possible interactions between several weakly penetrant mutations. Whatever the penetrance, these deleterious mutations have a direct impact on life expectancy of carriers (it shortens life time because of diseases that they favor at early ages). One might ask why natural selection, generation after generation, did not eliminate them. This is the issue of this article. To answer this question, the first paragraph describes the methods we used, the population parameter that were necessary, and how they were mixed together to provide an acceptable population-size evolution. The characteristics of the mutations that are introduced in the model are in accordance with the knowledge about BRCA mutations. A stochastic computer routine was developed to simulate what happens along generations to these mutations. First tests concerned the introduction of 5 mutations favoring cancer at different ages that do not provide any specific advantage about fertility. Second tests used various but relevant corrective measures to counterbalance the natural decline of mutations rate among studied population. In a second paragraph, these results are discussed in the light of what is known about BRCA mutations. Observational results are then described: they were obtained from a large database of family presenting with a hereditary cancer risk (more than 9 000 families and 190 000 family members recruited since 1985 in Centre Jean Perrin Oncogenetic Department). Limitations and further possibilities are described in the last chapter.

Materials and Methods

Because the economic changes of these last centuries did not concern all continents at the same time, researchers of more advanced countries could collect data that appear relevant to describe primitive population characteristics. Other works have investigated registries to constitute same king of data. From this data, different kind of pyramid of age can be found in the literature:

a) by INED, the French National Institute of Demography [4]for France and England (1750 and 1850)
b) by GLOBOCAN for Saharan Africa in 2002 for example [5].
c) In PROVIDE survey [6] for South-Africa

Most other parameters could be found in publications of the French National Institute of Demographic Studies (INED) or were extracted from a cohort (COSA) of 1962 women that we constituted in our region (middle France) between 1996 and 2006. Half of the women of this cohort were treated for breast or ovarian cancer and the other half constituted a control group seen for prevention consultation. Their age was comprised between 25 and 89 with an average equal to 58±10 (standard deviation) [7]. To facilitate the reading of following paragraphs, formulas are grouped in (Appendix 1).

Modeling the Risk of Death

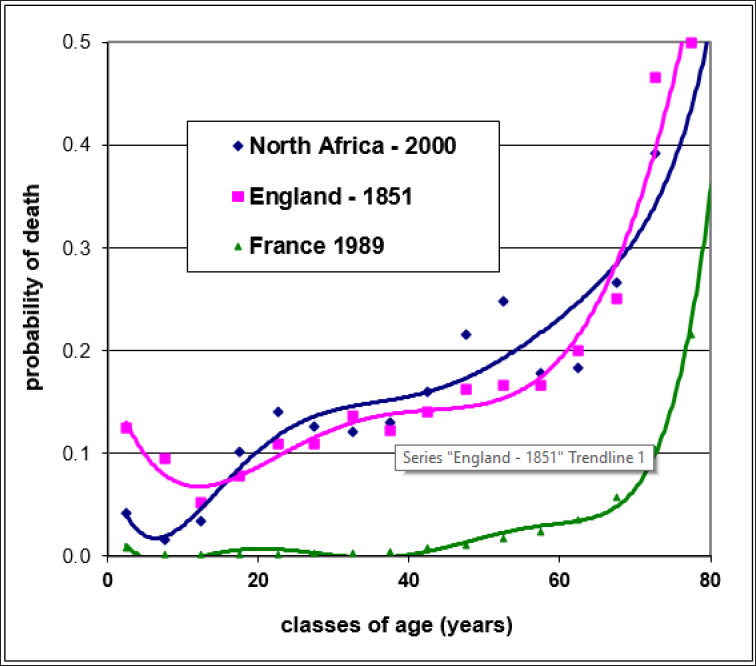
Although the simulations reported hereafter are performed in a primitive context, three patterns have been modelled: the mortality risk of primitive populations, the one of under-developed countries and the present one typical of industrial countries. The pyramid of age for England in 1851 was chosen to represent a primitive situation: it corresponds to a rather steady risk of death for males and females all along life, with the known high mortality risk during the first 5 years related to the infant mortality excess. The GLOBOCAN pyramid of age for North Africa that appears similar, already shows the impact of medical progress for the first classes of age, with a reduced probability to die during childhood. The former was used to model primitive context while the latter to estimate life expectancy in under-developed countries. Finally for industrialized countries, the 1989 French pyramid of age was used. After these choices, risk of death according to age was calculated, using a polynomial regression. (Figure 1) shows for females how the mortality risk differs depending on context.

Figure 1: Fitted curves for female mortality by 5-year classes of age and three different contexts.

Marriage

Marriage (rate and age) has social determinants whatever the civilization. For example, at the end of the 18^th century in France, celibacy was enjoined to 12% of women when they got nun and about 15% in main cities because of domesticity; earlier, at the end of the 17^th, childless women were estimated according to church registers between 6% and 7% [8]. In our COSA cohort, which represents modern occidental societies, 3.5% of women never got married or lived in couple less than 3 years and were nulliparous. A 4% celibacy rate was introduced in our model, but we had no means to check if this value was relevant in a primitive context. Somehow, a celibacy rate seems inevitable because of congenital abnormalities or other possible social rules, even in primitive groups that may forbid marriage to some individuals. The same celibacy rate was attributed to men, although it might sometimes be much higher, for instance if polygamy is permitted: females are therefore less available for bachelors and men remain more often alone. Polygamy could be set on in our modelling, but monogamy was the most tested situation. [9] found a mean age at first child of 25 with a standard deviation equal to 5 years.

We decided that this age was also relevant for wedding although one year could have been retrieved (at least 9 months before birth of first child). But in our modelling, it was possible to give birth to a baby just after the wedding, so this correction was not necessary. For primitive populations, we fixed the mean age of first wedding at 18±5: this agrees with the mean age at first birth that was 18.7 in rural women of Zimbabwe in 1980 [10]. Similar figures were reported by [11] in rural populations of eight countries of Southern and Eastern Africa. The minimum fertility age for females (menarche) was fixed at 13 years, under the null hypothesis. Men were considered fertile at the same age but because average wedding age for males is usually greater than females' one [9], we added 2 years in contrast to women's wedding mean age. Another reason for the older marriage age for men comes from the high maternal mortality rate causing men getting re-married at later ages. The mortality risk at each pregnancy reached 1.5% during Middle-Age [12] and such figures are still observed in some sub- Saharan countries conversely to developed countries where a 10/100 000 rate is common [13].

Natality Parameters: Number of Children

Natality corresponds to several parameters, but main statistics evaluate natality rate using fecundity rate per women. INED edited in 2004 a population survey comparing fecundity of French native women to North-African migrant women [14]. Another survey concerned households of South Africa in 1995 [6]. Both sources found a females' fecundity peak at 28-year. Data from Bangladesh contrasted from these previous outcomes [15]: fecundity peak of women between 1960 and 1976 was close to age of 22 years. The 28 years peak was nevertheless chosen although this could be discussed. An earlier fecundity period would shorten intergeneration intervals and would accelerate the modeled process. Our choice is thus more conservative (it does not interfere with events that we search for: it only delays them). We also considered that fecundity in women was a stable variable and neither social nor medical factors could let final fecundity rates vary. These parameters were used to compute the fecundity curve for primitive population. Another parameter, that does not seem to depend on social factors, is the miscarriage rate. This rate reduces significantly the final number of viable children. In our COSA cohort, this rate almost reached 20% of all pregnancies. Other population surveys have reported similar statistics [16-18]. Owing to the anti- apoptotic properties of BRCA genes, we made this rate variable to evaluate possible compensations for the deleterious role of tested mutations. The maximum absolute reduction of this rate was set to 10% although in a population-based analysis, this diminution reached one third [19].

Gender of Children and Mutation Transmission

Normally, to compensate for the higher male infant mortality, more males get born than female. In France, 105 males get born for 100 females, thus a probability to be a male of 51.2%. This percent was kept in our modeling. The chance for a child to receive a mutated gene from one of his parents is 50%. In our modeling, this value was set for each possible mutation.

Age of Menopause

In our COSA cohort, mean age of menopause was 51±3.8 years and its distribution were Gaussian. This age is rather stable worldwide: for example the same age was reported in a large Norway cohort [20] and a slightly younger age 49.3±3.4 in a large Japanese cohort [21]. This parameter is very important because reproduction period length (time from menarche to menopause) has a direct impact on natality outputs. In our model, we fixed the mean menopause age at 50±5 years. Of course, because of usual early mortality in primitive population, most of simulated women died before menopause. A limitation of male fertility must be questioned. A Canadian study based on ancient family registries [22] showed that male widows continued to get married and to have children even when they were 60 years old or more. In this survey, chosen old men were married with women younger than 30.

They contributed to an average of 2.2 children which was compared to 2.8 children for men married before they were 30. This small decline with age can be justified by studies of semen quality among men of various ages [23], that show a slight but constant yearly reduction after 30 years of sperm motility and concentration. However, this decrease happens to be inferior to the one due to environmental changes (nutrition, life habits, pollution...): for instance between 1973 and 1992 the decrease of motile and normal spermatozoa in fertile French men was higher among young adults of each period than the decrease caused by age. Other reproductive problems may occur also for older men such as congenital anomalies whose rate increases with age [24]. Considering also that a reduced correction of male fertility rate would be of insignificant value as it would apply to a very limited population (most of men die before 50 in a primitive context) in our modeling, no upper limit was fixed to male fertility age.

Cancer Risk and Incidence

Incidence and mortality of cancer statistics were available in FRANCIM report [25]. For women older than 20, the risk to develop a breast cancer according to age exhibited a peak between the ages of 60 and 64. In the COSA study, the peak was 58±12 years and distribution was almost gaussian. The cancer incidence curve to simulate cancer risk was set gaussian with a 5-year standard deviation, considering cancers caused by mutation happen much earlier and in a more grouped fashion. Breast cancer is supposed to induce death in the following 5 years in 30% of cases. This cancer stops rapidly fecundity. In our modeling, the end of fecundity (for both gender) was set at disease onset and we made the average delay till death equaled to 5±5 years although this is a very optimistic hypothesis. All cancers prognosis was supposed to follow the same gaussian shape. Penetrance is the cumulative rate of disease occurring in a population of mutation carriers. For BRCA mutations, penetrance is supposed to vary according to environmental conditions: for example BRCA penetrance is close to 70% today which means that 70% of mutated women will have a breast or ovarian cancer during their life-time.

Some life habits can change this penetrance (breast feeding, parity, nutrition, physical activity) and the BRCA penetrance was supposed to be much lower, around 50% one century ago. In our modeling, this parameter could be changed, but calculations reported hereafter were performed using a 50% penetrance. Sporadic cancers have also been considered, to better fit reality: indeed, main difficulty in population survey is often to distinguish between sporadic cancers and those favored by hereditary factors. An interesting work of [26] showed that most of cancers happen randomly at a frequency that increases proportionally with the number of cell divisions in tissues during life (correlation r = 0.81), therefore with age too. To implement the risk for sporadic cancer, we used epidemiological data reported by the department of UK cancer research 2012-2014 [27]. In case of competing cancer risk, that is a familial one associated to a sporadic one, the first occurring - most of the time the familial cancer - was kept. There is no biological reason to believe that this proportionality was different in the ancient times.

Mutations Geographic Spread Map

Simulations have also investigated how deleterious mutations dissemination could be influenced by geographical aspects. A virtual map was created, and individuals were randomly spread on it at the beginning. Travels across the map were limited by generation and distances were limiting factors for individuals to find a spouse. Different conditions were tested as for example mutations interacting in synergy or not regarding the cancer risk.

Complementary Parameters

We supposed that marriage lasted until death (no divorce), that marriage was not possible between brothers and sisters, parents and children, while more distant filiations were admitted forming new couples. After the death of a spouse, the widow could get married again, except menopausal women in order not to reduce men's descendance (as a man getting married with a menopaused woman would not expect a child). Polyandry was not implemented as it seems to be a very rare social rule in Man's history.

Randomization for the Monte-Carlo Simulations

Two algorithms were implemented:

a) the standard random function of Microsoft Visual Basic (a random table) with a pointer re-initialized by the timer function at the beginning of main loops.
b) Mersenne-Twister algorithm [28]: it is a validated algorithm that generates pseudo-random numbers.

Tests performed using both algorithms yield similar statistics, but the second algorithm was 10 times slower than the first one. For the calculations reported hereafter, the first algorithm was thus used.

Interface to Enter Parameters

A user-friendly interface enables to introduce calculation parameters. It includes:

a) Iterations number (default = 100)
b) Size of the initial population (2000 = 1000 females and 1000 males)
c) Length of the period during which the test is to be carried on (2000 years)
d) Time slice for the statistics (100 years), i.e. 20 checkpoints if period lasts to 2 millennia as above.
e) Type of mortality curve, i.e. age pyramid. We used here the primitive context.
f) Average fecundity per women (2.1 for a developed context)
g) Polygamy permitted or not (no)
h) Number of mutations to test (5)
i) Initial frequency of mutation carriers per mutated gene (5%)
j) Impact of these mutations on fecundity:
a. Miscarriage risk set to 20% (and decrease to 5%)
b. Marriage precocity (±2 years, default = 0)
c. Synergy between mutations: yes/no and number of mutations necessary for this synergy to work
k) Mutations penetrance (50%)
d. Synergy between mutations: yes/no and number of mutations necessary to make penetrance cumulative.
l) Gender concerned by the cancer risk (males, females or both)
m) Age peak for penetrance: the age when most cancers related to the mutation occur (40 years)
n) Progressive penetrance precocity (years): if 5 mutations are studied with a median peak for cancer susceptibility = 40 years, a 10-year precocity, would attribute to the first mutation a cancer risk peak at (40 - 2±10) = 20 years, and 30, 40, 50, 60 respectively to the four other mutations.

Verification

An EXCEL routine was developed to check how families were generated by our software: this routine enables to draw for each family the resulting pedigrees (Figure 2). The legend of the figure describes main symbols signification. Mutations are indicated using a lowercase letter added to the subject number when needed. Statistics consist in means and standard deviations calculated for each parameter over the total number of iterations. They are registered at each time slice, as for example every century if check points are scheduled by intervals of 100 years.

Figure 2: Partial view (4 generations) of a pedigree generated by our software and drawn using a VBA-EXCEL routine to ver-ify the shape of resulting families: female = pink rectangle, male = blue rectangle, orange = familial cancer + age at occurrence, yellow = sporadic cancer (none here), grey age at death and hatched = miscarriage.

Results

Results presented hereafter were obtained using simulations within a primitive context, considering this was the case most of the time homo-sapiens existed (>50 millennia). Also, only two millennia of evolution were evaluated by calculation, enough duration to notice already significant evolutions.

The most interesting trend concerned the mean age of cancer onset (marked by an arrow in (Figure 4B)). Year after year, this mean age increased until it almost reached menopause mean age. This highlights how selection pressure works: because carriers of mutations favoring the most precocious cancers die rapidly, their reproduction period is shortened, and their offspring is reduced. Thus, generation after generation, these carriers become less, and less numerous and worst mutations disappear. Precocious cancers then become rarer and mean age at cancer onset increases. This phenomenon tends to reduce the incidence of all major diseases happening before menopause. Hence, without any hypothesis about the etiology of cancers, it evidences that onset of cancers is likely to happen naturally near menopause or after. This selection happens also for men if partners' ages are often similar: but this relationship is indirect.

Tests with Five Deleterious Mutations Providing a Fertility Advantage

As concluded above, ancient mutations favoring early cancer in human should have disappeared with time. But it is not the case. Thus these mutations must have provided some evolutionary advantages. Two possibilities were tested in our simulations: they permitted to compensate for the loss of reproductive chances. The first one was a reduced miscarriage rate, and the second an earlier onset of reproduction period (i.e. by reducing first marriage age). As in (Figure 4), the two most deleterious mutations were eliminated during the first millennium, although penetrance was set at 50% (half of mutation carriers would have a cancer if they did not die before from another cause). First difference concerned the overall size of the population which grew steadily, especially when mutated women could get pregnant one year earlier: the global increase was 11.3% for (Figure 5A) and 20.4% for (Figure 5B) versus 5.6% in figure 4 when no compensation was introduced. Interestingly, non-mutated individuals seemed to benefit as others from the reproductive advantage of slow penetrant mutations. Final proportion of mutation carriers were respectively 15.5% when the advantage was a 5% miscarriage risk reduction and 17.3% if reproduction begun one year earlier. As 3 of the 5 mutations remained at the end of the follow-up period, it suggests the proportion of mutation carriers should increase in the following millennia, especially for the latter advantage. 

Beti Bachao Beti Padhao Program to Save the Girl Child-Educated the Girl Child: Impact Analysis of Government of India Flagship Program in Uttar Pradesh, India  - https://biomedres01.blogspot.com/2020/02/beti-bachao-beti-padhao-program-to-save.html

More BJSTR Articles : https://biomedres01.blogspot.com