An Optimal Robin-Type Domain Decomposition Method for Raviart-Thomas Vector Field in Three Dimensionsn

An Optimal Robin-Type Domain Decomposition Method for Raviart-Thomas Vector Field in Three Dimensionsn

Introduction

In this paper, we consider the following boundary value problem

(1.1)

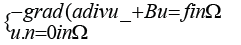
Given a bounded convex polyhedral domain Ω ⊂ R3 , we introduce the boundary value problems where a∈L∞ (Ω) is a scalarvalued positive function bounded away from zero, the coefficient matrices 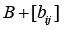 is symmetric uniformly positive definite with  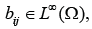1 ≤ i j ≤ n and f ∈L2 (Ω)3 . The weak formulation of problem (1.1), and the study of the Raviart-Thomas finite elements, as well as our iterative method, require the introduction of an appropriate Hilbert space H(div;Ω) . It is given by

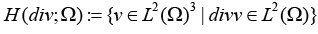
which equipped with the inner product (.,.)div;Ω; and the associated graph norm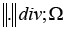 defined

by

The subspace of vectors in H(div;Ω)with vanishing normal component on ∂Ω is denoted by

H0(div;Ω) and it is the appropriate space for the variational formulation of (1.1):

Find u∈H0 (div;Ω) such that

where the bilinear form a(.,.) is given by

We associate an energy norm, defined by 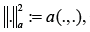 with the bilinear form; our associations on the coefficients guarantee that this norm is equivalent to the graph norm. Given a vector u∈H(div;Ω), it is possible to define its normal component u. n on the boundary [1].

LEMMA 1.1.

Let Ω ⊂ R3 be Lipschitz continuous. Then, the operator 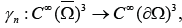 mapping a vector into its normal component on the boundary, can be extended continuously to an operator  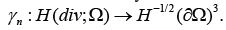In addition, there exists a continuous lifting operator  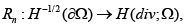such that  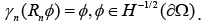The following Green’s formula holds, u∈H(div;Ω) and q∈H1(Ω),

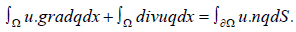
where the integral on the right hand side is understood as the duality pairing between 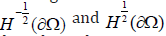. We consider finite element discretization’s based on the Raviart-Thomas elements. For triangulations made of tetrahedra, the local spaces on a generic tetrahedron K are defined as

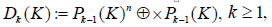
where x is the position vector in Rn and Pk-1(K) is the space of homogeneous polynomials of

degree k−1 on K. A function u in Dk (K) is uniquely defined by the following degrees of freedom

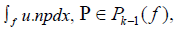
for each face for each face f of K. For k > 1, we add

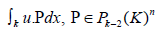
It can be proven that the following spaces are well-defined:

The corresponding interpolation operator is denoted by 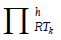 When there is no ambiguity,

we simply use the notations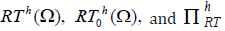 

For the case k = 1, the elements of the local space have the simple form

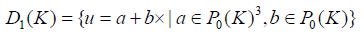
It is immediate to check that the normal components of a vector in D1 (K) are constant on

each face f. These values

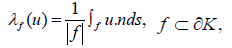
can be taken as the degrees of freedom.

The spaces H(curl;Ω) and H(div;Ω) , and special finite element approximations have been introduced to analyze equations such as (1.1); see [2]. In recent years, a considerable effort has been made to develop optimal or quasi-optimal, scalable preconditioners for these finite element approximations of problems in H(curl;Ω) and H(div;Ω) . Two-level overlapping Schwarz preconditioners for these spaces have been developed for two (see [3]) and three (see [4- 10]) dimensions, respectively. Multigrid and multilevel methods are considered in [11-28]. A few papers on the H(curl;Ω) case have proved optimality for a two-subdomain iterative sub structuring preconditioner, combined with Richardson’s method, for a lowfrequency approximation of time-harmonic Maxwell’s equations in three dimensions. In [19] the authors restrict themselves to two dimensions and develop an iterative sub structuring method for the problems in space H(curl;Ω) . In their work the condition number bound is independent of the number of substructures, it is developed locally for one substructure at a time and therefore insensitive to even large changes in the coefficients from one substructure to its neighbors.

Domain decomposition (DD) methods are important tools for solving partial differential equations, especially by parallel computers. In this paper, we shall study a class of nonoverlapping DD method, which is based on using Robin-Robin boundary conditions as transmission conditions on the subdomain interface. There is some iterative Robin-Robin DD method in the literature. This method was first proposed by Lions. Actually, the optimal transmission condition on the interface involves a nonlocal operator, which is not convenient to implement. So, adopting some local approximations to this operator becomes a useful way, which usually result in Robin-type boundary conditions. Some interesting Robin-type transmission conditions are considered in [21] for elliptic problem, and in [23] for the Helmholtz problem, respectively. Higher order approximation is also studied in [9], where they use the Pade approximates to localize the operator. However, the higher of approximation order, the more additional costs it has. The convergence was proved to be 1−O(h) in [16,25]. Then, in [29], Gander, Halpern, and Nataf improved it to be 1−O(h1/2 ) in the case of two subdomains. Later, Qin and Xu gave the convergence rate1−O(h1/2H1/2 ) in many subdomains. Later, Qin and Xu gave the convergence rate 1−O(h1/2H1/2 ) in many subdomain cases in [30], and further they used the Dirichlet-to-Neumann operator to prove that the convergence rate cannot be improved. A sharp convergent result is also obtained in [31-35]. For the case of arbitrary geometry interface, Liu also got the convergence rate to be 1−O(h1/2 ) in [22]. For the second-order Robin-type transmission condition, the convergence rate was improved to 1−O(h1/4 ) in [36]. Recently, for the two subdomain case, a new two-parameter Robin-Robin DD method was proposed by Chen, Xu, and Zhang in [37]. It is shown that the convergence rate is independent of the mesh size h without any additional computation. For the discontinuous coefficients problem, the convergence of the optimized Schwarz method was analyzed in [19] for the two subdomains case. In [30,31], the authors introduced some preconditioned systems of the optimized Schwarz method. In [29], the authors present a new Robin-type nonoverlapping domain decomposition (DD) preconditioner, and they have proved the preconditioner is optimal and scalable.

In this paper, we restrict ourselves to three dimensions and develop a preconditioner for equation (1.1). The preconditioner is induced from the Robin-Robin domain decomposition (DD) algorithm. We have proved that the condition bound is independent of h, so the method is optimal. To analyze the bound of the condition number, it has been necessary to obtain a continuous extension from the trace space ofH(div;Ω) into it, which has been constructed in [38]. The outline of this paper is as follows. In section 2, we will describe our Robin-Robin DD algorithm. In section 3, we will describe our preconditioner induced from the renew equation of the algorithm. In section 4, we will consider its corresponding condition number estimate. The implementation of this new DD algorithm will be discussed in section 5. Finally, some numerical results to verify our theoretical results will be given in the last section.

Model Problem and DD Algorithm

Problem (2.1) is equivalent to the following coupled problem, the equivalence can be proved

by considering the corresponding variational problems.

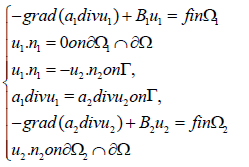
where the first transmission condition is chosen based on the fact that only the normal components of the finite element functions are continuous across the interelement boundaries, see [39,45]. The transmission conditions of (2.1) is equivalent to the following Robin-Robin boundary conditions:

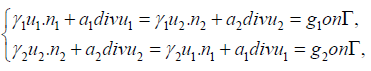
where we allow γ1 ,γ2 to any positive constants such that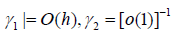 

Let 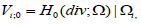multiply the first equation of (2.1) by  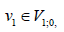and integrate it

over Ω1, we get

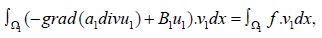
by parts, with the Green’s formula, we get

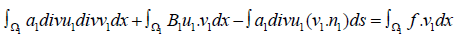
Using the boundary condition (2.2), we get

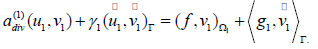
This way, we get the second variational problem on Ω2 :

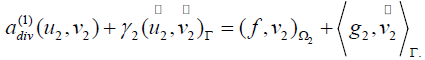
Where

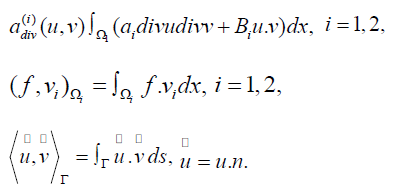
Definition (The Robin-Robin DD method.) Given 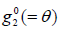 on Γ a serial version domain

decomposition iteration consists the following five steps (m=0,1, ...):

a) Solve on Ω2 for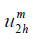 

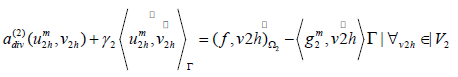
b) Update the interface condition on Γ :

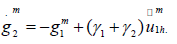
Get the next iterate by a relaxation:

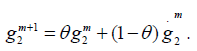
The Preconditioner Induced from the DD Algorithm

Let 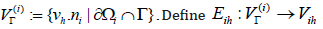 as follows:

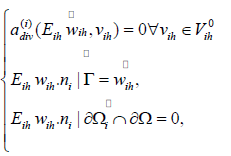
Where 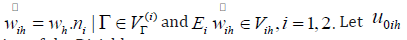 be the solution of the Dirichlet

problem:

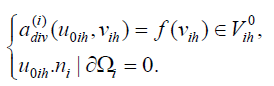
Define Sih to be a linear operator on VΓ which satisfies the following equations:

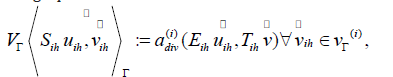
Where 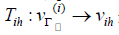 is any extension such that  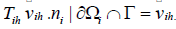Define fih satisfies

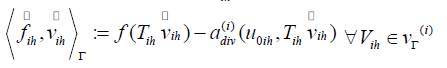
The definition of sih and fih is independent of the choice of Tih for all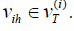 

Note that 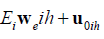 satisfying:

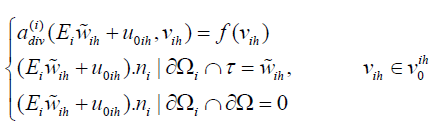
Based on Lax-Milgram theorem the solution of the problem is unique, i.e.

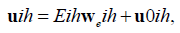
so that,

Therefore (2.3) and (2.4) are equivalent to

Because of the of the arbitrariness of vih, we obtain

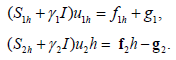
The Robin-Robin Iteration is equivalent to

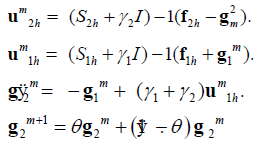
We induce that

Where

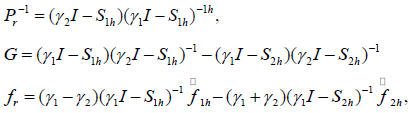
which shows that the renew equation of the Robin-Robin algorithm is a preconditioned Richarson iteration for the following equation:

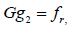
where the preconditioned operator is Pr−1

We notice that

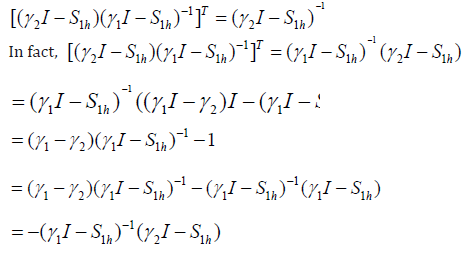
In the same way,

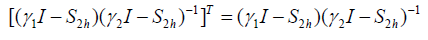
Thus, the operators G and Pr−1 are symmetric and Pr−1 is positive definite, G is also positive

definite will be proved later. Therefore we can use the preconditioned conjugate gradient (PCG)

method to solve the system.

The Condition Number Estimate

LEMMA 4.1. For the discrete harmonic extension operator Eh, we have (deduced from Theorem 2.5 in [32], or Lemma A.19 in [7])

LEMMA 4.2: It holds that

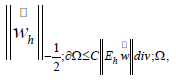
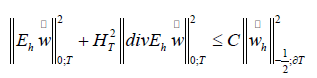
Proof. The proof is similar to one given in [24, Lemma 4.3]. We will first prove the result for a

substructure T of unit diameter. Consider a Neumann problem:

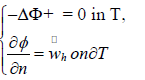
Here 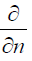 is the derivative in the direction of the outward normal of ∂T. Define an extension operator  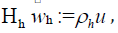where u = gradeφ, and ρh is the interpolant onto the Raviart-Thomas space Xh(T), defined by the degrees of freedom of Xh are given by the averages of the normal components over the faces of the triangulation:

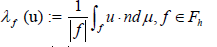
Where |f| is the area of the face f and the direction of the normal can be fixed arbitrarily for each face, we will show below that they {λf(u)} are well defined. Using the surjectivity of the map φ →∂φ onto Hs(T) and a regularity result given in [9, Corollary 23.3], we deduce

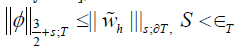
where ∈T is strictly positive and depends on T.

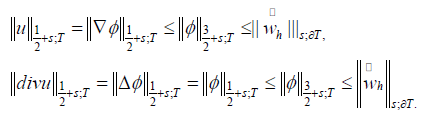
They {λf(u), f ∈ Fh} are well defined, since 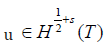 , with s > 0, then

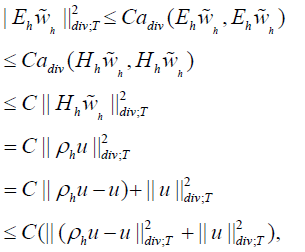
Where 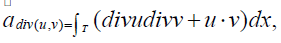 and Rn is the extension of Lemma in [3].

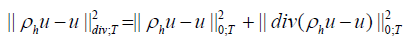
We find that

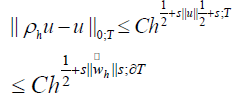
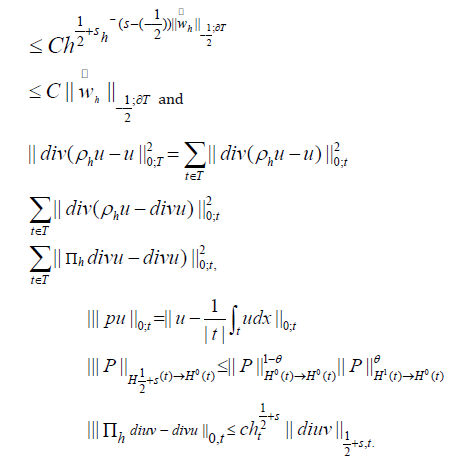
Where,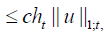 

is the L2 projection onto the space of constant functions on each fine 

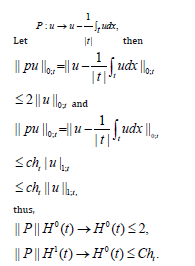
By interpolation theory, we have

Employing an inverse inequality, we find that for s <∈T ,

therefore,  We now consider a substructure T of diameter H, obtained by dilation from a sub structure of unit diameter. Using the previous result and by using a scaling argument, we have

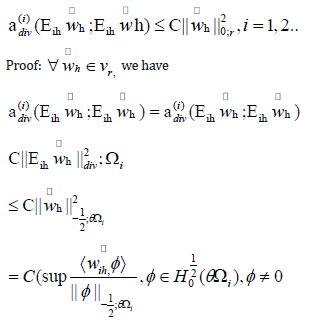
Theorem 4.3.

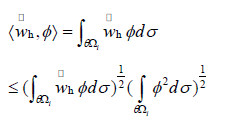
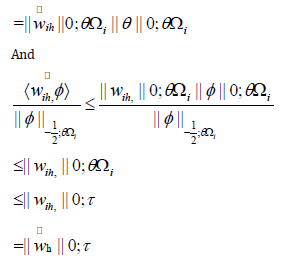
Therefore

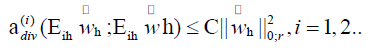
Theomem 4.4. It holds that

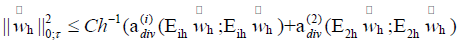
Proof we find that,

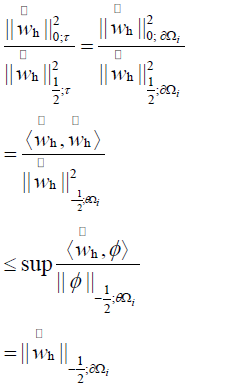
By inverse inequality, we have

(4.3)

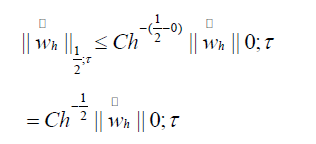
Combining (4.2), (4.3), and Lemma 4.2, we obtain

(4.4)

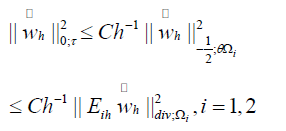
The final result is obtained by summing (4.4) over i = 1, 2

Theomem 4.5:

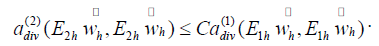
Proof. Based on Lemmas 4.1, 4.2, and the equivalence of the energy norm and graph norm, we

have,

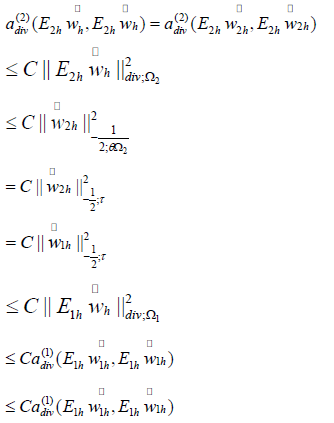
LEMMA 4.6. It holds that

Based on the definitions in section 3, we have,

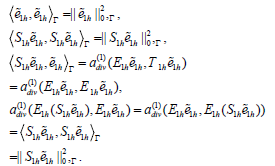
Combine (4.6), (4.7), (4.8) with (4.9), (4.10), (4.11), (4.12), we obtain,

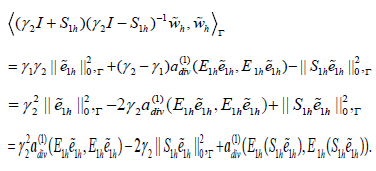
Thus we have,

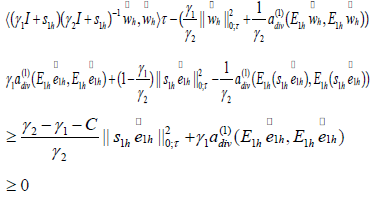
that is the left part of (4.5). On the other hand,

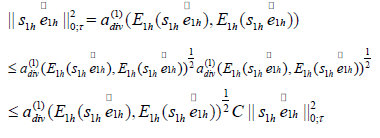
Thus,

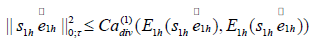
Finally, based on the above inequality, we have

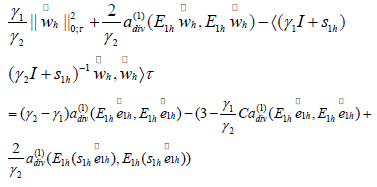
In the above inequality, we use the fact that  for sufficient small h. So

we have proved the right part of (4.5).

LEMMA 4.7. It holds that

Based on the definitions in section 3, we have,

Combine (4.14), (4.15), (4.16) with (4.17), (4.18), (4.19), (4,20), we obtain,

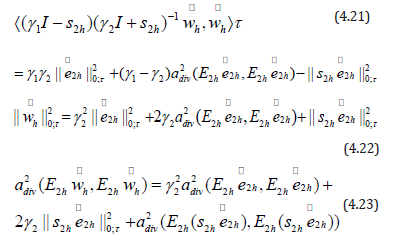
Applying Lemma 4.3 and (4.21), (4.22), (4.23), we have,

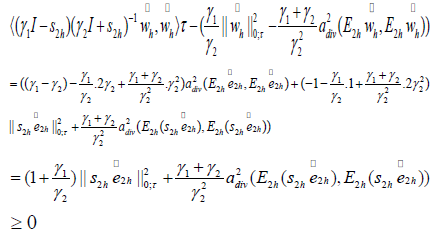
that is the left part of (4.13). On the other hand, we have

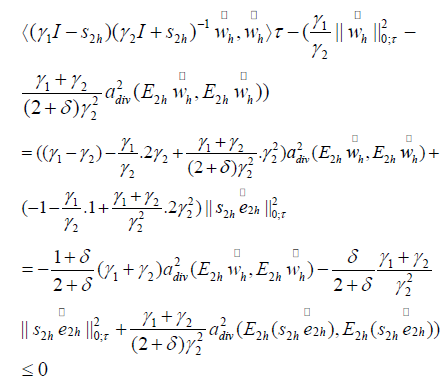
so we have proved the right part of (4.13). Based on Lemmas 4.6 and 4.7, we have Lemma 4.8.

LEMMA 4.8. It holds that

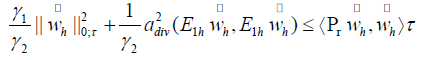
Based on Lemmas 4.2, 4.3 and 4.8, we get the following main result of this paper.

THEOMEM 4.9. Assume that 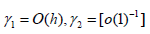 then,

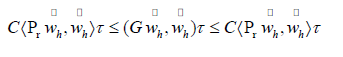
Numerical Results

In this section, the convergence behavior of our new DD method will be checked by some numerical experiments. Consider the problem

(5.1)

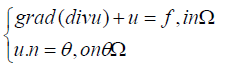
Where,  and the function

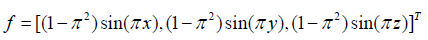
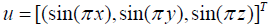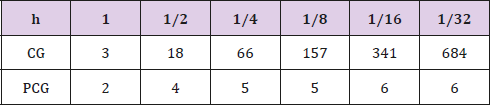
The exact solution of this problem is  The domain Ω is divided into 2 subdomains. We set the Robin parameters to be γ = h,2h , γ2 = 50,100 which satisfy the condition of Theorem 4.9. The iteration stops when 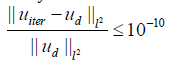 (Figures 1-4) and (Tables 1-4).

Table 1: Iterative number of γ1 = h and γ2 = 100.

Table 2: Iterative number of γ1 = 2h and γ2 = 100.

Table 3: Iterative number of γ1 = h and γ2 = 50.

Table 4: Iterative number of γ1 = 2h and γ2 = 50.

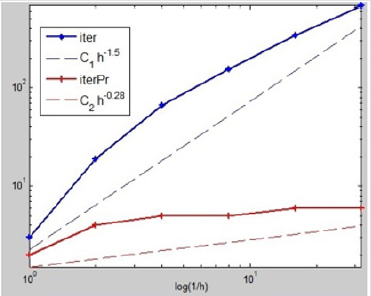
Figure 1: The figure describes the case of γ1 = h and γ2 = 100, where the ordinate values of these nodes on these polylines are iterative numbers which are the dates from Table 1, while the abscissa values of these nodes are the corresponding log(h). And the red ones describe the calculation processes with our precondition, while the blue ones describe the corresponding processes without our precondition. The dashed lines approximate the slopes of the corresponding polylines.

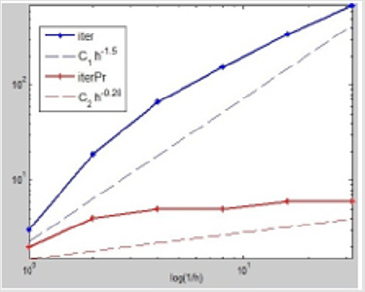
Figure 2: The figure describes the case of γ1 = 2h and γ2 = 100, where the ordinate values of these nodes on these polylines are iterative numbers which are the dates from Table 2, while the abscissa values of these nodes are the corresponding log(h). And the red ones describe the calculation processes with our precondition, while the blue ones describe the corresponding processes without our precondition. The dashed lines approximate the slopes of the corresponding polylines.

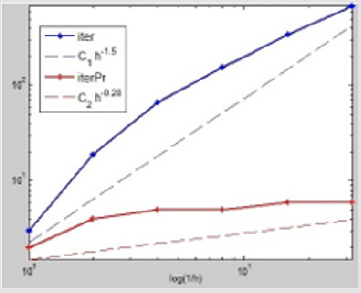
Figure 3: The figure describes the case of γ1 = h and γ2 = 50, where the ordinate values of these nodes on these polylines are iterative numbers which are the dates from Table 3, while the abscissa values of these nodes are the corresponding log(h). And the red ones describe the calculation processes with our precondition, while the blue ones describe the corresponding processes without our precondition. The dashed lines approximate the slopes of the corresponding polylines.

Figure 4: The figure describes the case of γ1 = 2h and γ2 = 50, where the ordinate values of these nodes on these polylines are iterative numbers which are the dates from Table 4, while the abscissa values of these nodes are the corresponding log(h). And the red ones describe the calculation processes with our precondition, while the blue ones describe the corresponding processes without our precondition. The dashed lines approximate the slopes of the corresponding polylines.

It is seen that as h decreases, the iteration numbers do not increase, which confirm our theoretical results reflect that our preconditioner is efficient and this preconditioned DD method is optimal.

Acknowledgement

We thank the anonymous referees who made many helpful comments and suggestions which lead to an improved presentation of this paper.

For more Articles on: https://biomedres01.blogspot.com/