A Hierarchical Reduced Markov Model for Reliability Evaluation of Phased-Mission Systems

A Hierarchical Reduced Markov Model for Reliability Evaluation of Phased-Mission Systems

Introduction

Many practical systems, such as those encountered in electronic, aerospace and nuclear power have multiple phases of operations during their mission and are generally referred to as Phased-Mission System (PMS) [1]. Compared with general system, the reliability evaluation of PMS is much more complicated because of the components dynamic behavior as well as their dependence across the phases. Considerable efforts have been made in the analysis of PMS. Generally, existing methods can be roughly classified into two groups: Analytical methods and simulation methods [2]. The analytical methods are further classified into combinatorial approaches, state-based approaches, hierarchical approaches and modularization approaches. The combinatorial approaches, especially the binary decision diagram-based algorithm [3,4], exploit the Boolean algebra to reduce the model scale, which are effective in evaluating non-repairable PMS. The state-based approaches are mainly based on Markov model [5,6], which suffers from the state-explosion problem when is applied to large-scale systems. The simulation methods typically offer greater generality in system representation, but they suffer from computational inefficiency and great computer memory consumption [7].

The above-mentioned methods mainly apply to small-scale PMSs due to the high computational complexity. This paper proposed a reduced Markov reliability model by using hierarchical reduction techniques. Compared with the traditional Markov model, the proposed method can efficiently reduce the number of system states, and avoid the well-known state-explosion problem. The remainder of the paper is organized as follows. Section 2 describes the hierarchical reduced Markov model. Section 3 illustrates our method with a specific example. Lastly, section 4 concludes the study and discusses future works.

The Hierarchical Reduced Markov Model

It is common that the real engineering systems provide hierarchical feature which can be used to advantage in the PMS reliability analysis. For example, thrust subsystem for an aircraft frequently effect all phases of a mission, maybe in different quantities, at each stage of flight [8]. Furthermore, the top-level subsystem can be decomposed into lower level components such as compressor and turbine runner. Such structure is common in many other engineering systems, not just those relating to aircraft. The hierarchical architecture is also a usual style in software reliability estimation, in which systems are decomposed into different layers according to the components’ calling relations [9]. And it is also used to describe the interpreter relations of different layers in communication software. Accounting for hierarchical structure in the phase failure logic will enable a more reduced Markov model to be developed. One way of taking advantage of these features is using hierarchical reduction method which can reduce the state space of Markov model efficiently by subsystems replacement. The main idea of this method is generating a hypothetical component to replace the top-level subsystem. The components of subsystems are considered to be all in series or in parallel. Thus, the failure rate and repair rate of the hypothetical component can be derived by manipulation of the corresponding components’ parameters in the subsystem. Also, it is important that the subsystems replaced need to be totally independent of all other sections of the mission failure fault tree.

The detailed process of the hierarchical reduction method is discussed taking a n components subsystem for example. Let λi and μi be the failure rates and repair rates of component Ci . Also, λs and μs are the failure rate and repair rate of hypothetical component Csrepresenting the subsystem.

1) if the n components are series, λs can be given as

Let As denote availability of the subsystem, where is defined by

A series system is working when all of the components do not fail. If state 1 represents that all components are operational and 1 A is the steady-state availability of system in state 1, then A1 can be computed as follows.

Since state 1 is the only working state in series system, it can be derived that. As = A1 Moreover, according to Eq. (2) and (3), we have

From Eq. (1) and (4), we can use the hypothetical component Cs with failure rate λs and repair rate μs to replace the series subsystem.

2) if the n components are parallel, μs can be given as

For parallel system, the formula of availability As is presented in [19] as follows.

in which Ai = μi/λ +μi is the availability of component ci . Hence, using Eq. (2), (5) and (6), we obtain

From Eq. (5) and (7), we can use the hypothetical component cS with failure rate λS and repair rate μs to replace the parallel subsystem.

Case Study

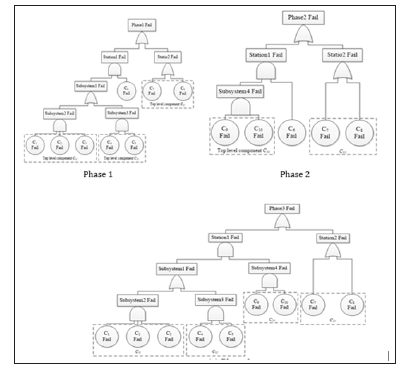
In this section we describe a case study to verify the proposed reduced Markov model for PMS reliability analysis. The mission reliability of the PMS has been calculated by the traditional Markov method. The example PMS is a space flight Telemetry, Tracking and Control (TT&C) system. The failure fault trees of the example TT&C mission are shown in Figure 1, in which station1, station2, and station3 are composed of c1~C6, C7~C8, and C9~c10 respectively. Assume that the failure rates and repair rates of components c1~c10 are unchanged across phases. The relevant parameters are detailed as follows: failure rates μi=3.33×10-3 ; repair rates μi=3.33×10-2; phase transition time t1 = 20s , t2 = 120s and t3 = 85s .

Figure 1: The failure fault tree of the three basic phases.

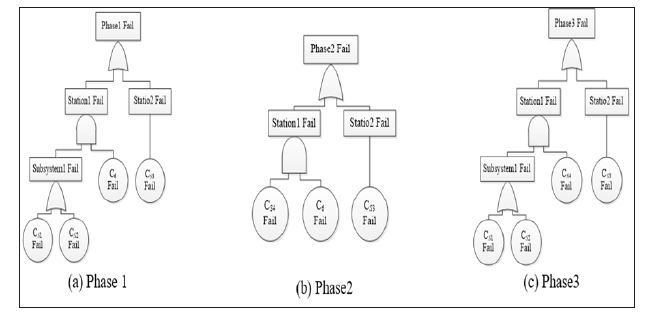
By analyzing fault trees of the three basic phases, there are four subsystems can be reduce using hierarchical reduction method. These are S1with components c1,c2 and c3 , S2 with components c4 and c5 , S3 with components c7 and c8 , and S4 with components c9 and c10 . Therefore, the top level subsystems S1 , S2 , S3 and S4 can be replaced by four hypothetical components cS1 , cS2 , cS3 and cS4 respectively. For the series subsystem, failure rate and repair rate of the top-level components can be computed by using Eq. (1) and (4). Similarly, Eq. (5) and (7) can be used for the parallel subsystem. The computed parameters of the top-level hypothetical components are presented in Table 1. After hierarchical reduction, the new PMS phases configuration is shown in Figure 2.

Table 1: Computed parameters of the hypothetical components (unit: min).

Figure 2: New phases configuration of the PMS after hierarchical reduction.

From Figure 2, we can derive that the number of reduced system states of the three phases are 16, 8, and 16 respectively. For the original PMS, these are 256, 32, and 512 respectively. Because the number of components is decreased efficiently by using hypothetical components to replace the top-level subsystems, and it will slow down the increase in transition rate matrix scale. The PMS reliability and computation time of the traditional Markov method, and the hierarchical reduction method are presented in Table 2. The computing errors of each phase between traditional method and the hierarchical method are shown in Figure 3. Results in Table 2 indicate that there is an excellent match between the proposed method to the traditional Markov method, with relative error less than 1.19×10-5. Furthermore, the computation time of our method is less than the traditional Markov method. This is mainly because that the number of system states of simplified Markov model is less than that of traditional models. However, from Figure 3 we can see that the computing errors increase dramatically with the mission time. Thus, the hierarchical reduced Markov model is applicable for short duration PMS.

Conclusion

This paper presents a reduced Markov model using hierarchical reduction approach to evaluate the PMS reliability. The traditional Markov model suffers from the problem of huge transition rate matrix. Our approach takes advantage of PMS provide hierarchical feature, and an simplify the original Markov model of each phase by hierarchical reduction. In comparison to the traditional Markov approach, the proposed method achieves less time cost, also has good computation accuracy. However, the hierarchical process may cause computation errors. In future work, more attention will be addressed on error analysis, and efforts should be made to improve current method to achieve more accuracy and efficiency.

Respiratory Muscle In Post-Polio Syndrome: Highlights-https://biomedres01.blogspot.com/2020/08/respiratory-muscle-in-post-polio.html

More BJSTR Articles : https://biomedres01.blogspot.com