Monte Carlo Simulation in Radionuclide Therapy Dosimetry 

Introduction

Monte Carlo [MC] method is a modeling tool, capable of achieving a close adherence to reality, concerning the analysis of complex systems. Generally is a method for estimation of the solution of mathematical problems by means of random numbers like those obtained by a roulette-like machine in gambling casinos [1]. Radiation transport processes like absorption and scattering are determined by the Boltzmann transport equation. The evolution of the distribution density in μ space, is described by Boltzmann’s transport equation which can be analytically solved in oversimplified situations. MC techniques have been proposed for solving Boltzmann equation by simulating the interaction of particles with matter, using stochastic methods [2]. It is very useful for complex problems which cannot be resolved by deterministic methods. A physical process comprises individual probabilistic events that are simulated sequentially. These events are governed by probability distributions statistically sampled to describe the total process.

Therefore, a large number of trials are required to describe adequately the physical phenomenon. Considering particle interaction, this method follows every single particle emitted from a source to its death (absorption, escape, etc.). Probability distributions are randomly sampled to determine the outcome at each step of every particle life, using transport data. In MC method, solutions are obtained by simulating individual particles and recording some aspects (named tallies) of their average behavior rather than solving an explicit equation. The information required from tallies depends on user’s request. A complete reference of tallies can be found in article [3].

Historical Retrospection of Monte Carlo Simulation

MC method is generally attributed to scientists working on the development of nuclear weapons in Los Alamos during the 1940s. However, its roots go back much further. The idea of simulation could be attributed to Compte Georges Louis Leclerc de Buffon, in 1772 [4]. The problem to solve was the probability P that a segment of length L randomly positioned on a plane would intersect one line of a set of parallel straight lines at distance D>L apart. Theoretically, the probability is given by P = (L/D) / (π/2). Buffon tried to experimentally check the above expression by actually drawing parallel lines and throwing a needle on the floor of his house. This experiment was actually the representation of a device for the computation of π. Lord Kelvin also appears to have used random sampling to calculate time integrals of the kinetic energy that appear in the kinetic theory of gases.

In the last century, Enrico Fermi invented a form of the MC method when he was studying the moderation of neutrons, in Rome. Although, he did not publish anything, he was frequently formulating his predictions. During the II World War, Fermi joined other scientists to develop the first atomic bomb. One of them, Stanislaw Ulam having a keen interest in using sampling techniques to neutron diffusion studies, realized that this method was impractical without the development of computers, because it was tedious and time consuming [5]. He described the idea to John Von Neumann, and they began to plan actual calculations. Essentially, they ran experiments on Los Alamos computers and sought their solutions through following many individual neutrons along their histories. As it was about a secret government project, a code name should be invented. Von Neumann chose as his reference the Monte Carlo Casino in Monaco because of the resemblance of statistical sampling techniques as in neutron diffusion studies- with games of chance, where randomness could be resolved in predictable probabilities.

Monte Carlo Methods in Nuclear Medicine

Monte Carlo [MC] method was first introduced by Snyder at Oak Ridge National Laboratory in order to assess the fraction of photon and electron energy emitted from radionuclides in source tissues, deposited in various target tissues. With the design of the first mathematical model of the human body, Walter Snyder at the Oak Ridge National Laboratory used MC method to track γ-rays and x-rays from radionuclides within various source tissues and assess the fraction of their emitted energy that is locally deposited in various target tissues [6]. This was the concept of absorbed fraction, defined within the newly conceived Committee on Medical Internal Radiation Dose (MIRD), a method of internal dosimetry. Values of specific absorbed fraction were tabulated for a variety of source and target tissues combinations and were later used to calculate the so called S- factors [7]. The S-factor was initially calculated for the Reference Man that is for geometrically shaped organs [8,9]. In the decade of 1980, the specific absorbed fractions were optimized because of the introduction of mathematical phantoms by Cristy and Eckerman, encompassing adult, child and pregnant anatomy [10,11]. These values are the basis for MIRDOSE and OLINDA/ EXM software [12,13]. The OLINDA code was written by Dr. Stabin. It is based on the MIRDOSE 3.0 and 3.1 codes (predecessors of the OLINDA code) developed by Dr. Stabin. The OLINDA/EXM® personal computer code performs dose calculations and kinetic modeling for radiopharmaceuticals (OLINDA/EXM stands for Organ Level Internal Dose Assessment/Exponential Modeling). OLINDA employs essentially the same calculation algorithms as MIRDOSE, with some updates that include: Nearly 600 new radionuclides (including alpha emitters), new organ phantoms, a revised and improved bone model, the ability to modify organ masses to patient-specific values. OLINDA® calculates radiation doses to different organs of the body from systemically administered radiopharmaceuticals and performs regression analysis on user supplied bio kinetic data to support such calculations for nuclear medicine drugs. Calculations are performed by simulating some thousand decade photon histories, a value limited by the computer resources of that time.

Values are quite accurate but the models they refer are very simple. Application of reference S-factors may induce errors because anatomical details vary among patients. As an alternative, the convolution of cumulated activity distribution with a dose point kernel using Monte Carlo is proposed [14]. This approach is fast and takes into account the geometry of a given patient. However, it may introduce errors when applied to varying tissue densities as dose point kernels are calculated for particles propagating in uniform medium (e.g. water, soft tissue). Patient-specific dosimetry, based on MC simulation methods, using up to 100 million photon histories, has been investigated by several groups [15,16]. Dosimetry by MC simulation for each patient is more accurate, as S-factors can be calculated, taking into account anatomic individualities as well as the physical properties of the radionuclide.

Imaging of patients to obtain anatomic and physiologic information has advanced greatly in the past decade [17]. Anatomic information obtained with Magnetic Resonance Imaging (MRI) or Computed Tomography (CT) is usually expressed in three dimensions in voxel format, with typical resolutions of 1mm order. Similarly, SPECT and PET imaging systems can provide threedimensional (3D) distributions of activity inside patients, also in voxel format, with typical resolutions of around 5 to 10 mm. Modern systems combining CT or MRI with SPECT or PET modalities allow for 3D dose estimation in each voxel, if an appropriate radiation transport method is applied. MIRD Pamphlet No.17 has introduced voxel dosimetry to allow dosimetric calculations at the voxel level [18,19]. The use of a well-supported radiation transport code such as MCNP or EGS4 with knowledge of patient anatomy could result in a significant improvement in the accuracy of dose calculations [20-22]. The capability for performing radiation transport in voxel phantoms with the MCNP or EGS4 Monte Carlo radiation transport codes for internal sources has been demonstrated in [23-27]. The PEREGRINE code has also been proposed for 3D computational dosimetry and treatment planning in radio immunotherapy [28]. In a study, the calculations of energy deposition at the voxel level performed by different MC codes (MCNP4C, EGSnrc and GEANT4) for radionuclide targeted therapy dosimetry have been investigated and compared [29]. The MCNP4C code is an extended version of the originally developed MCNP code to treat electron transport, as well as neutron and photon transport. The EGS (ElectronGamma-Shower system) is a general-purpose package for the MC simulation of the coupled transport of electrons and photons in an arbitrary geometry for particles with energies above a few keV up to several hundreds of GeV [30]. The EGSnrc MC code implements significant improvements in the physics of radiation transport with respect to EGS4. GEANT4 is a general-purpose toolkit that simulates the transport of several particle-types in a wide range of energies. It was originally developed for simulating high energy physics experiments, but nowadays it is also used in various areas of application, including medical physics.

GEANT4 allows the simulation of a comprehensive set of physics effects, such as hadronic, electromagnetic and optical processes. It has been found that, if dose estimations with voxelized S formalism are performed, variations among different MC codes are expected to be within a few percent. However, in cases of radionuclides that low-energy electrons cover an important part of the emission spectrum, more consistent differences may be obtained and can affect considerably dose depositions at small distances. Calculation of electron and isotopes dose point kernel has been the main subject of various studies [31,32]. Therapies with radiopharmaceuticals using beta- or alpha-emitter radionuclides are growing significantly and very fast. In internal dosimetry β- and α+ emitters are used for therapeutic applications to deliver high dose rate on tumors. Modified MC codes have been used for simulation therapy with beta emitters (β-) applied on the tumor cells [33-35]. For small tumors and micro-metastases, the electron energy which escapes the tumor volume cannot be neglected and must be calculated for the specific radionuclide, tumor mass and shape. The absorbed fractions in tumors with small radii are greater with low energy beta (β-) emitters and alpha (α+) emitters [34]. Moreover, heterogeneity of intra-tumoral distribution of administered radionuclides leads to non-uniform absorbed dose. An accumulated Dose Volume Histogram (DVH) showed that most tumor cells received a lower dose than average tumor absorbed dose [36]. This discrepancy between conventional and cellular approach show that dosimetry on cellular level is necessary for a better selection of radionuclide and optimal calculation of administered activity in the radionuclide therapy.

Use of Voxel Models / Monte Carlo Simulations in Nuclear Medicine

Traditional internal dosimetry is based on the use of fixed geometry phantoms to derive S values for absorbed dose estimation. Other phantoms for dosimetric calculations are the voxel phantoms family, human models based on Computed Tomographic (CT) or Magnetic Resonance (MR) images obtained from high-resolution scans. Voxel models introduced during the last two decades are derived mostly from medical image data of real persons. They consist of a huge number of volume elements (voxels) and offer a clear improvement over the MIRD-type mathematical phantoms. The standard phantom geometry was modified to include on-line MC calculation and therefore the ability to introduce tumors and adjust organ masses and shapes. Voxel phantoms can be applied in radionuclide therapy; though, to determine patient specific absorbed doses for every individual patient, a special phantom is necessary. With the improvement of segmentation procedures, the creation of a phantom is quick and can be completed in a couple of hours. A disadvantage of Fixed Geometry Models is that do not match the actual patient anatomy. This is addressed by developments in 3D imaging-based patient specific dosimetry software [37,38]. For internal dosimetry of photons, β- and α+ particles, the parameters influencing the organ doses are mainly the relative position of source and target organs (for photon organ cross-fire) and organ mass (for organ self-absorption). International Commission on Radiological Protection (ICRP) has decided to use voxel phantoms for the update of organ dose conversion coefficients that will follow the ICRP Recommendations. These voxel phantoms should be representative of the male and female reference adult with respect to their external dimensions, organ topology and masses. Therefore, according to the ICRP philosophy, a new set of conversion coefficients has been evaluated [39,40].

The use of voxel models in MC radiation transport codes has contributed to the improvement of dose calculations. OEDIPE software based on MCNPX code was developed by the “French Institut de Radioprotection et de Sûreté Nucléaire” (IRSN), in order to investigate the body burden from internal contamination [41,42]. The GSF-GOLEM model was coupled with the FLUKA MC Radiation transport code for space dose assessment [43]. FLUKA MC code used to perform patient-specific 3D dosimetry through direct MC simulation on PET-CT and SPECT-CT images. Results were compared with those obtained with the voxel kernel convolution method and with other Monte Carlo-based tools. The absorbed dose maps were compared at the voxel level. The use of FLUKA for patient-specific, image-based dosimetry in nuclear medicine is now available [44]. Voxel MC Model (VMC) software was also developed allowing a large variety of subject-detector configurations [45,46]. Furthermore the Voxel man model was merged into MCNP code [47]. A voxel head model was created for the calibration of in vivo monitoring systems for bone seeker radionuclides [48] by Italian ENEA-Radiation Protection Institute.

Aspects and Future Potential/MC Simulation/Nuclear Medicine

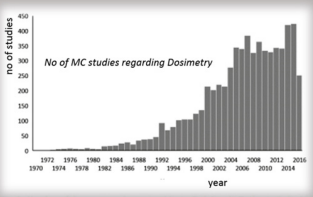
Individualized of medical protocols can be achieved by combining MC simulations with anthropomorphic computational models and clinical anatomical data. In Nuclear Medicine Therapy dosimetric applications by MC simulation, different tools are used for modeling realistic clinical acquisitions with accurate dose evaluations. Reliable simulations of particles in internal dosimetry are compared with experimental data. Many different dosimetric protocols are reported for individualized dosimetry and simulations of radionuclide therapy dose in nuclear medicine, with the use of modern computational phantoms. The incorporation of clinical data and computational models can provide a reliable tool for accurate dosimetry calculations. New generation of dose modelling tools have been developed for use with internal emitter therapy in nuclear medicine. Patient specific 3D dose distributions, based on a fusion of anatomical (CT or MRI) and functional (SPECT or PET) data, with individualized MC calculations can be obtained in a reasonable amount of time using high powered computing workstations or distributed computing networks. The combination of realistic computer phantoms and accurate models of the imaging process allows the simulation of nuclear medicine data be ever closer to actual patient data. Simulation techniques find an increasingly important role in the to-day of nuclear medicine for development of personalized computer phantoms, the accurate 3D modelling of projection data and quantification of them. According to Scopus (www.scopus.com), the relevant documents in ‘‘Dosimetry” and ‘‘Monte Carlo” are almost 7000 in the last 45 years, as shown in Figure 1 [49], From Dosismetry applications in GATE Monte Carlo toolkit, by Panagiotis Papadimitroulas http://dx.doi.org/10.1016/j. ejmp.2017.02.005, 2017 Conclusively, accurate simulation process and verification via comparison with experimental and patient data is essential for quantitative measurements of absorbed dose, tumor and critical organ volumes in order the radionuclide therapy schedule be the most precise.

Figure 1: Number of Monte Carlo studies in dosimetry applications in time period 1972 to 2016.

More BJSTR Articles : https://biomedres01.blogspot.com/