Biomechanical Investigation of Different Tying Forces on Knot Security

Biomechanical Investigation of Different Tying Forces on Knot Security

Introduction

Wound closure by suturing is practiced frequently among all clinicians. Knot failure including knot slippage and suture breakage is the most common failure mechanism that prevents wound recovery back to their original anatomical positions [1,2]. Wound dehiscence can potentially complicate wound healing. One major factor determining knot failure is its security [3]. Knot security is defined as the survival of a suture knot after a continuous load has been applied [4,5]. A poorly secured knot has a higher chance of failure at the knot as the knot is the weakest point of the suture [6-9]. Many studies have investigated various factors affecting knot security. Eric et al. investigated the effects of different surgical knotting techniques, suture materials, suture sizes, and number of throws on knot security of square, surgeon’s, and sliding knots used in oral and maxillofacial surgery [4]. Similar studies were carried out by Lo et al. [10] and Ilahi et al. [11] for arthroscopic soft tissue repairs. All of the studies confirmed that the knot security of different knotting techniques that had undergone static or cyclic testing can possess different biomechanical performance.

However, surgeons’ fatigue towards the end of the day and tie knots with inconsistent forces [12]. Tying a force too loose or too tight can affect the knot security and hence have negative effects on wound healing [13]. Knowing the optimum force required to tie a secure knot would be a step closer in making sure that knots are tied consistently. To the best of our knowledge, the relationship between tying force and knot security has yet been studied. In the present study, we propose an experimental set-up that enables testing of a knot configuration which is tied with a measured force. This setup mimics the situation when surgeons are fatigue and have the tendency to tie knots with inconsistent forces. We hypothesize that there is an optimum tying force to tie the most secure knot.

Materials and Method

Specimen Preparation

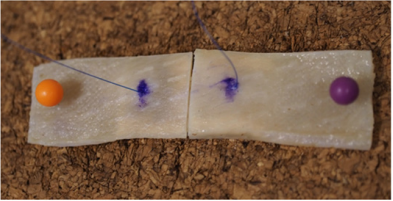
Fresh frozen porcine skin was used in the experiments. The porcine skin was defrosted to room temperature using 0.9% saline solution before conducting the experiment. It was cut to a size of 140x15mm Figure 1. A laceration was made in the middle of the porcine skin along a longitudinal direction to simulate a complete open skin wound. Each side of the porcine skin measured 70x15mm. Prolene 4-0 (Ethicon, US), a single stranded synthetic nonabsorbable polypropylene monofilament suture was used to stitch the skin. The surgeon’s knot was chosen as the knot technique of choice in our study because it is a simple and commonly adopted knot technique that has been shown to be superior to square and sliding knots in terms of knot security [4, 14-16]. For each specimen, a surgeon’s knot with 3 throws (2-1-1) was made. The distance of the stitch to the edge of the wound was kept constant at 10mm. Five tying forces, 1N, 2N, 3N, 4N, 5N were adopted to tie the suture. A tolerance of 0.5N was controlled at each tying force. This would give a range of the tying force, i.e. 1±0.5N. Ten samples were tied using each force giving a total of 50 samples.

Figure 1: Specimen of porcine skin 70x15mm. A longitudinal laceration was made and a 10mm distance from the edge to the suture was kept constant.

An Instron 3343 (Instron Corp., Canton MA, USA) mechanical tester was used to measure the tying force. As shown in Figure 2, the suture was looped around 2 metal bars one on top of the other. For the 2nd and 3rd throw, the suture was looped around the bottom bar first, pulled upward and rounded the upper bar with a controlled downward force. Based on the force equilibrium, both upward and downward tension of the suture gave the resultant force as measured by the mechanical tester. Hence, the actual force for knot tying would be half of the force that was being measured, eg 2N would be pulled to 4N. However, we did not measure the force of the first throw as making a simple cross of suture without any taut could not warrant a stable enough force to measure. Therefore, only forces of the 2nd and 3rd throws were measured.

Figure 2: The suture was looped around 2 metal bars one on top of the other. For the 2nd and 3rd throw, the suture was looped around the bottom bar first, pulled upward and rounded the upper bar with a controlled downward force.

Biomechanical Testing

Cyclic Testing: Cyclic tests were performed on E-1000 Dynamic Tester (Instron Corp., Canton MA, USA). After suturing the porcine skin with the respective forces, the ends of the porcine skin were mounted onto pneumatic grippers with blasted clamping surfaces. The distance between the two grippers were maintained in such a way that the specimen would not be taut figure 3. Cyclic testing was divided into 2 stages. Stage I comprised of the 1st 100 cycles with a loading force of 2-10N. Stage II was the 2nd 100 cycles with a higher loading force of 2-20N. A frequency of 1Hz was used to cyclically load the specimens under both stages. Both knot slippage and suture breakage was considered as the failure criteria of the tests. For knot slippage, a 6mm elongation of crosshead displacement is chosen according to the study done by Baums et al. [9] A high resolution video recorder was used to record the failure mechanisms in knot security.

Figure 3: After completing the suture, the specimen was placed in between 2 pneumatic grippers such that the specimen would not be taut.

Survival rate of surgeon’s knots in Stage I and II was calculated as followed: (number of specimens that survived after 100 cycles of the stage)/10. A bar graph showing survival rate against tying force is presented in Figure 4 and 5.

Figure 4: Survival of knots at stage I.

Figure 5: Survival of knots at stage II.

Static Testing: Surgeon’s knots that survived cyclic testing were subjected to static testing. The knot was pulled to failure at a rate of 20mm/min. Ultimate tensile strength (UTS) needed to pull the knots to failure were recorded.

Statistical Test: Mean and standard deviation were calculated for the sutures subjected to static testing. Student t test was conducted to calculate the p value. A p value less than 0.05 is statistically significant.

Results

Cyclic Testing

With a cyclic force of 2N-10N in stage I, tying forces of 3N and 4N had the highest survival rate of 100% Figure 4. Tying force of 1N was the least desirable with a survival rate of 60%. Tying force of 2N achieved a survival rate of 70% and 5N achieved a survival rate of 90%. When the cyclic force increased to 2N-20N in stage II, 3N tying force retained the highest survival rate of 90% Figure 5. Tying force of 2N was the least desirable with a survival rate of 20%. Tying force of 1N achieved a survival rate of 40%, 4N achieved 40% and 5N achieved a survival rate of 60%.

Static Testing

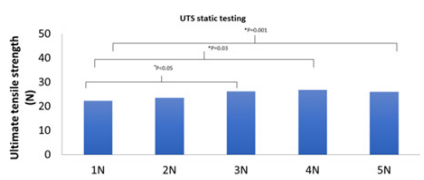
As shown in Figure 6, knots tied with 4N that survived cyclic testing had the highest mean UTS of 26.8N while knots tied with 1N that survived cyclic testing had the lowest mean UTS of 22.3N. Statistical testing showed that UTS of tying forces 3N, 4N, 5N were significantly different (p<0.05) when compared to UTS of tying force 1N. UTS of tying forces 1N, 3N, 4N and 5N were not significantly different (p>0.05) when compared to UTS of tying force 2N.

Figure 6: UTS of knot failure with different tying forces. (*) shows a statistically significant difference between groups.

Failure Mechanisms in Knot Security

Knot slippage caused all tested knots to fail during cyclic testing. For static testing, all knots failed due to suture breakage at the knot.

Discussion

In this study, we investigated 5 different tying forces i.e. 1N, 2N, 3N, 4N, 5N. We took 5N tying force to be the limit because pulling to a force greater than 5N (actual force = 10N) was difficult to achieve. We chose Prolene 4-0 as the suture material for surgeon’s knot for 2 reasons: the UTS of the suture material Prolene is not high and easy to slip due to its smooth surface. We are of opinion that using a slippery suture material with low mechanical strength for simple knotting technique such as a surgeon’s knot can validate our experimental setup so that it can be easily adopted for testing other suture materials and knotting techniques. For cyclic testing, we divided the test into two stages. Stage I comprised the 1st 100 cycles with a cyclic load of 2-10N while the 2nd 100 cycles with 2-10N were tested in stage II. Baum et al. [9] suggested to divide cyclic testing of knot security into 8 power levels with an increase in 10N for each level for every 100 cycles up to 80N. This was unnecessary in the present experimental setup because all of the Prolene 4.0 broke by the tensile load in between 20 – 30N, based on the static testing results.

As shown in Figure 4, all knots tied had a survival rate of more than 60%. In particular, 3N and 4N had a survival rate of 100%. Hence, we suggest that the optimum range of tying force is 3N and 4N under the cyclic loading below 10N. On the other hand, it is also possible to include 5N tying force in the optimum range since its survival rate stood at 90%, which is very close to a survival rate of 100%. We are of opinion that 1N and 2N tying forces could be insufficient to tie a knot, which resulted into a lower survival rate (60% for 1N tying force and 70% for 2N tying force). For stage II, increment of the cyclic load would affect the optimum tying force and hence the survival rate. As shown in Figure 5, the survival rate of knots tied with 3N tying force dropped to 90% but was still the tying force that obtained the highest survival rate. In fact, the survival rate of other tying forces also dropped. 1N tying force achieved 40%, 2N tying force achieved 20%, 4N tying force achieved 40% and 5N tying force achieved 60%. We were aware that 4N and 5N tying force had 60% and 30% drop in their survival rates. This could be attributed to the reason that tying a suture with too much force can in turn cause the suture to be even weaker due to a decrease in knot security.

On the other hand, the 1N and 2N tying force had a 20% and 50% drop of their survival rates respectively. We believed that too loose a knot would give it no holding strength when subjected to greater cyclic load. Our initial thoughts were that the best performing tying forces were to follow up from stage I. However, the experimental results showed that 4N tying force had the most significant drop in survival rate. This could be inferred that different knot tying forces would perform independently under various cyclic loading conditions. Therefore, 3N was still the optimum tying force because it achieved the highest survival rates under different cyclic loads.

An ideal biomechanical test of knot security is one that best simulates reality. Rarely would a patient pull a wound with a single large force. Wound dehiscence occurs due to continuous forces applied to a suture throughout the day. In our study, static testing revealed that tying forces between 3N to 5N could achieve the highest UTS before suture breakage. However, this contradicted cyclic testing results which showed that tying knots with 4N and 5N did not achieve significantly better results. Hence, we could confirm that the cyclic testing is a more physiological testing method to investigate the knot tying.

Previous studies have shown that a wide range of tying forces are used amongst expert surgeons [17-20]. Stefan Neuhofer et al demonstrated that the overall range of tying force used by surgeons regardless of suture technique and thread type was 3N - 63N with a mean of 15N [17]. However, knots were tested by pulling the knot to failure using a single load. With this span of varied forces, it is difficult to know what exactly the correct range of tying force is. Our study has shown that 3±0.5N tying force would give a secured knot. A knot with more dedicated tying force improves the precision and also reduces the chance of knot slippage in clinical practice. This can help prevent abnormal scar formation which can be aesthetically distressing to many patients [21]. It is also important to recognize that the force used to suture a knot cannot be too low or too high. Rodrigues et al study showed that small intestines started to damage at 1.6N and rupture at 2.1N, whereas large intestines start to damage at 2.2N and rupture at 3.0N [22]. Similar for skin suturing, we are of the opinion that a suture tied using large forces would be painful, cause tissue damage, tissue scarring and even result in subsequent infection [23]. Knowing the optimum force can guide a clinician how much force should be exerted when tying a knot at any time of the day.

There are limitations to our study. Firstly, we have found that 3±0.5N is the optimum range of tying force that should be used to tie a knot, but this force can only apply to a surgeon’s knot with 3 throws tied with Prolene 4.0. Further studies must be done to find out the optimum force that is needed to tie a different material, knot technique and number of throws. Secondly, our study only applies to instrument tied knots such as Minimal Invasive Surgery. There are many knots in clinical practice that are hand tied. Thus, it still remained a challenge to determine how much force is used in a hand tied knot. Thirdly, although porcine skin is widely used in suturing studies, it is difficult to ensure that porcine skin can mimic human skin. For eg, the texture, thickness and tension might be different. Furthermore, skin at different locations have different tensions. Since different tissue types have their own individual range of acceptable forces before damage occurs [21], the force used to tie a knot might differ in skins at different sites with different characteristics. In this study, the first throw of the surgeon’s knot was not measured.

The first throw had no taut when tied as it was to keep the suture in position. Regardless of the force used to tie the first throw, the suture would still be loose. Lastly, as this was an in vitro study, it only took into consideration the force required for knot slippage. The optimum force required to preserve other factors of skin healing such as vascularity was not considered.

Conclusion

we present a new experimental setup to test a knot configuration with different tying forces. Based on the static and cyclic testing, we found that 3±0.5N is the optimum range of force needed to tie a surgeon’s knot with 3 throws for maximal knot security using Prolene 4.0.

Acknowledgements

This study was supported by the Singapore Ministry of Health’s National Medical Research Council under its Centre Grant (NMRC/ CG/M011/2017) and the Surgery Academic Clinical Program grant (Biomechanics Lab Programme). The authors would like to thank Mr Zeus Lim Yi Wei, BSc from Biomechanics Laboratory for his helps with manuscript preparation and submission.

For more Articles on: https://biomedres01.blogspot.com/