Recent Advances in Experimental Methods of Cellular Force Sensing

Abstract

Anchorage-dependent cells are active biomechanical systems that constantly sense and generate biomechanical forces. Such cell-generated biomechanical forces are known as traction forces exerted by cells on their underlying substrates or intercellular stresses generated between neighboring cells in a cell sheet. While there are many cell-generated force sensing techniques available, researchers frequently utilize traction force microscopy (TFM) and monolayer stress microscopy (MSM) to compute cell-substrate traction forces and cell-cell intercellular stresses, respectively. In this short review, we will explore recent advances in TFM and MSM methods and their impact on cellular functions in vitro. In addition, we will discuss the advantages and limitations as well as prospects of these novel methods in cell mechanics.

Keywords: Mechanobiology; Cellular biomechanics; Biomechanical forces; Traction force microscopy; Monolayer stress microscopy

Introduction

Living cells employ a diversity of feedback mechanisms during their lifetime and generation of biomechanical force is one of them [1-3]. Biomechanical forces at the cellular level impact biological functions of the cell such as cellular growth, development, division, adhesion, and progression of pathological processes [4-6]. In addition, biomechanical forces generated by cells such as pushing, pulling or crawling are particularly important during their physical interaction with underlying extracellular matrix (ECM) and with their neighboring cells [1-5]. To quantify cell-generated biomechanical forces, researchers have developed several in vitro experimental techniques. These force sensing techniques are either force sensing at the cell-substrate level or force sensing at the intercellular level [3-5]. Forces produced at the cell-substrate level are actomyosin mediated contractility passed to the ECM via focal adhesions of the cell and are commonly known as traction forces or simply as “tractions” [2-5]. On the other hand, forces at the intercellular level are due to physical interactions between neighboring cells in a collective cell sheet and are known as “intercellular stresses” [7- 9]. In recent years, traction force microscopy (TFM) and monolayer stress microscopy (MSM) methods are successfully implemented to quantify biomechanical forces at both cell-substrate level and intercellular level, respectively [3-5,7-9]. Although the extent of this short review will not cover all the experimental techniques used in cellular force sensing, we will summarize the concept of 2D TFM and MSM method, recent advances using these force sensing techniques, advantages and limitations of these tools and their future in the field of cellular biomechanics.

Determination of Tractions at the Cell-Substrate Level

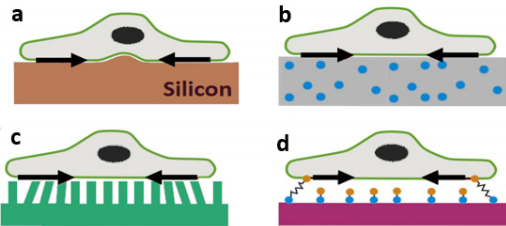
The basic concept of TFM starts with computing the deformation produced by cells on a soft substrate [1-4, 5]. Early attempts were mostly to use a thin sheet [1]. However, the non-linear response of material made quantitative evaluation complicated [1,3]. To resolve this issue, researchers started to use thin silicon films (Figure 1a) or polyacrylamide gels (PA gels) which can easily deform due to cell contractility [10,11]. Silicon films buckles under the cell and PA gel surface has immobilized fiducial markers (Figure 1b) which can be tracked using fluorescent microscopy techniques. With the knowledge of film movement or fiducial markers displacement from their original position, traction fields can be obtained by solving the inverse problem of elasticity theory [10-12]. Another TFM approach is to use microfabricated pillar arrays that work as strain gauges (Figure 1c) and deflection of the pillars give a proportional traction readout [13]. Unlike PA gels where cells form unconstrained adhesion, this method is limited with adhesion sites due to specific pillar topology [1,3,13].

Another alternative is to use molecular force sensors where an elastic linker is connected to cell domains [14]. This method is known as Förster resonance energy transfer (FRET) and gives direct fluorescent stress sensor readout as an equivalent measure of force due to elastic linker stretching by cells (Figure 1d). However, the local environment and difficulty associated with force sensors may cause errors in results [1,14].

a) Single cell on top of a thin film that buckles due to cell contraction,

b) Cell on top of a PA gel with fluorescent beads,

c) Cell on top of micropillar arrays,

d) Depiction of molecular force sensor in cell mechanics

Figure 1: Schematic representation of different TFM setup. Figure adapted from [1].

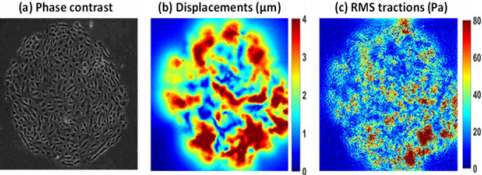
Among all the TFM methods available in the literature, the most popular one is with PA gels where fluorescent markers (generally <1 μm in diameter) are embedded in the substrate gel [3]. PA gels have a wide range of elasticity (from <1KPa to more than hundred KPa) [3,4] and gel thickness ranges usually anywhere between 20-200μm [3]. In those TFM experiments, gel surfaces are coated with an ECM that allows cell attachment on the surface [3-5]. As the experimentation progresses, fluorescent images keep a record of bead positions with cells on top. However, a reference image is required to compute displacements from fluorescent images taken at various time points [10-12]. Therefore, cells are removed at the end of the experiment to obtain a reference or “stress-free” image. Then displacements are calculated by comparing every other fluorescent image with the reference image. Finally, combining displacement measurements with the knowledge of substrate mechanical properties surface tractions are computed [10-12] (Figure 2).

a) Phase contrast image of a human umbilical vein endothelial cell (HUVEC) monolayer (diameter 1.25 mm) on top of a PA gel (stiffness 1.2 KPa),

b) Corresponding displacement field obtained by comparing fluorescent bead image with reference image in MATLAB,

c) RMS Tractions obtained from displacement field using a mathematical model described by Butler et. al. [12]. Tractions are represented as root mean squared (RMS) tractions (RMS traction = sqrt ((traction_x)2+ (traction_y)2). Data courtesy: Steward lab from University of Central Florida.

Figure 2: Displacements and RMS tractions obtained using TFM.

Over the past four decades, TFM methods have been successfully implemented in cell migration, wound healing and cancer metastasis studies [3-5,15]. A notable study with human metastatic breast, prostate, and lung cancer cell lines showed increased tractions in metastatic cancer cells compared to non-metastatic cells [16]. Bloom et. al. tracked the 3D trajectory of a migrating tumor cell and found elastic and reversible matrix deformation at the leading edge of the cell while trailing edge showed irreversible matrix deformation pattern [17]. Both studies prove that migrating pattern of tumor cells are different and more devastating than their normal counterparts. It has been found in several studies that cell-generated tractions are dependent on substrate stiffness and matrix stiffening can alter cell behavior [18-20]. For example, one migration study by Onochie et. al. with human corneal limbal epithelial cells concluded that increased substrate stiffness may affect epithelial cell tractions during healing response in certain corneal pathologies [21].

Additionally, there are quite a few studies performed on TFM platform probing cell motility under the influence of different hormones or drugs [3-6,22]. Jang et. al. exposed confluent MadinDarby canine kidney (MDCK) cells to hepatocyte growth factor (HGF) of various concentrations and found lower tensions in MDCK cells at higher HGF concentration [23]. Similar findings are expected during endothelial to mesenchymal transition (EMT) which is important in cardiovascular disease progression [23]. Our group has shown that tractions generated by human umbilical vein endothelial cells (HUVECs) are influenced by gap junction Cx43 communication [24]. In our study, we used a chemical known to disrupt Cx43 communication in a dose-dependent manner and observed lower tractions with a higher level of Cx43 communication disruption [24]. Our findings contribute to the knowledge of various cardiovascular complications arises in mammals due to Cx43 deficiency. Although a few TFM studies summarized here do not grasp the full accomplishment using the technology, it certainly depicts TFMs wide range of biological and biomedical applicability in the field of cell mechanics.

From Cell-Substrate Forces to Intercellular Stresses

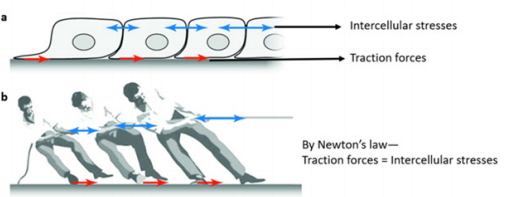
An important sub-field of TFM is determining cell-cell intercellular stresses from cell-substrate tractions by using the idea of force balance in a cell monolayer [8]. The concept is known as monolayer stress microscopy (MSM) and can be easily understood with an example of tug-of-war contest where the tension or pulling force generated in the rope are equivalent to the pushing force on the ground (Figure 3b) [8,9]. Similar concept can be applied to a monolayer of cells where cell substrate tractions are balanced by cell-cell intercellular stresses in a 2D cell plane (Figure 3a) [25]. MSM starts with the cell-substrate traction forces of the cell sheet and then performs a straightforward force balance within the entire monolayer as demanded by Newton’s law [7-9, 25]. This method doesn’t require the knowledge of the mechanical properties of the monolayer itself, rather only the knowledge of traction forces inside the optical field of view (i.e. inside the monolayer) gives intercellular stresses by Newton’s law [25]. Usually a computational tool such as finite element analysis with proper boundary conditions performs the force balance within the monolayer [8,9,25]. Then intercellular stresses inside the entire monolayer are known with their corresponding pixel locations. Intercellular stress distributions are generally rugged, heterogeneous and distributed throughout the monolayer (Figure 4).

a) Local tractions (red) applied by cells are balanced by long range intercellular stresses (blue)

b) Illustration of force balance using a tug-of-war contest. (adapted from Trepat et al. [25])

Figure 3: Concept of force balance in monolayer stress microscopy.

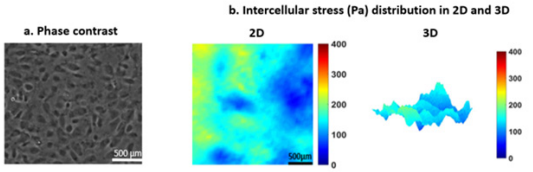
a) Phase contrast image of a HUVEC monolayer

b) Illustration of intercellular stresses (Pa) at both 2D and 3D showing rugged, heterogeneous stress distribution in the HUVEC monolayer. Bar 500 x 500 μm. Data courtesy: Steward lab from University of Central Florida.

Figure 4: Intercellular stress distribution in a HUVEC monolayer.

Intercellular stresses are crucial for understanding collective migratory behavior of cell which is important for many cellular processes such as wound healing, cancer metastasis or tissue repair [5,15,25]. For example, endothelial cells form the inner lumen of the vasculature [26] and their collective migratory behavior is important to protect the body from harmful substance. Hardin et al. showed that in the presence of agonists and antagonists endothelial force correlation length increases and decreases, respectively, suggesting endothelial barrier integrity are impacted by the presence of agonists and antagonists [27]. In another study, they also reported that in response to an agonist endothelial gap formation is linked to endothelial intercellular stress generation [28]. Tambe et al. reported that epithelial or endothelial cells tend to migrate along the orientation of the local maximal principal stress where shear stresses are set to be zero [8,25]. However, when cell-cell junctions are disrupted using calcium chelation cells do not migrate along the maximum principal stress orientation [25]. In another cell migration study, Cho et al. probed epithelial cell monolayer under the influence of electric field and were able to increase cell migration speed and their findings suggest that epithelial migration may be guided by electric potential [29]. Ultimately, the knowledge we obtain from tractions and intercellular stress analysis further increases our understanding of fundamental cellular processes such as collective migration, wound healing, angiogenesis, immune response, tissue morphogenesis [2-5,25,30,31].

Advantages and Limitations of TFM and MSM

TFM is widely popular because of simplicity and smooth laboratory setup. While, traditional TFM analysis is 2D in nature and ignores tractions in the z-direction, 3D TFMs calculate tractions in all cartesian axes. Although 3D TFM provides more traction information than 2D, they are far more complicated and computationally intensive [3,4]. 2D TFM provides fast data processing and reliable results and therefore more popular than 3D analysis. In addition, TFM offers live imaging thus making it possible to observe any phenotypical change in cells during experiments. Furthermore, both 2D and 3D TFM are not cell-specific. Therefore, tractions and intercellular stress analysis is possible for any anchorage-dependent cells. Although, availability of adequate number of fluorescent beads at the gel surface remains a key issue in traction measurement, using a high density of fluorescent beads into PA gels may resolve the issue.

Since tractions forces are obtained by comparing fluorescent images with a reference image, cells need to be removed to obtain the reference image. Caution must be taken during removing the cells as one may cause an unwanted shift (i.e. microscope stage or petri dish movement) from the original position and may lead to erroneous traction measurements.

In MSM, monolayers are treated as “continuum” and their microstructures are ignored [8,9,25]. Therefore, MSM doesn’t provide stress analysis for each individual cell, rather gives stress landscape for the entire monolayer. In addition, MSM suffers from “boundary effect” and as a result stress concentration may appear at the monolayer boundary edges [7,24]. However, boundary effect can be avoided by performing intercellular stress analysis over a region smaller than the original size of the monolayer (Figure 4a) and away from the monolayer boundary [9,25].

Conclusion and Future Aspects

In this short review, we explored some applications of TFM and MSM in the field of cell mechanics. Undoubtedly, cells are highly capable of regulating their biomechanical interactions with their extracellular environment in both normal and diseased condition [4]. Therefore, the analysis of biophysical forces could differentiate between healthy and pathological states of cells. In recent years, TFM has become an effective platform for integrated biomechanical and biochemical analysis in vitro. Many TFM models are now capable of microfluidic analysis as well as force probing in vitro. Shortening the computational time will improve the efficiency of existing 3D TFM models. Another excellent future addition will be the ability of real-time tracking of traction generation. This will provide new information about cell motility and biomechanical behavior under various biological situations. In the future, a TFM platform equipped with both force probing technology and biochemical testing capability will be a key tool to understand critical cellular mechanotransduction processes in vitro.

For more Articles on: https://biomedres01.blogspot.com/