Application of General Information Model to DNA Identification
Introduction
Research on DNA sequences is the focus of modern life science. Analysis of statistical attributes of DNA sequences is significant for evolutional biology and for technologies to identify living organisms. Several attempts have been made to identify relatively small size (microbial) genomes by using the distribution of the appearance of short consecutive nucleotide strings of length k called k-tuple [1-7]. To describe the distribution, many scholars used information quantities including Shannon entropy and Fisher information [8-16]. Some scholars also utilized some nonlinear methods or models to analyze the DNA sequences [17,18]. In this paper, we generalize the geographical remote sensing information model [19] to a general information model which is image joining equation calculated. Such model is a grey non-linear equation that is from formal logic inferring to dialectical logic calculation and from abstract thinking to both of abstract and visual thinking [19]. We apply the general information model to deduce four kinds of information quantities used in DNA sequence analysis and then analyze the statistical results cited from Ref. [15] on the scope of similar rules.
General Information Model
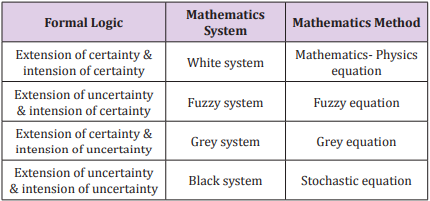
The remote sensing information model is established according to geographical regularity and complexity. This model, a grey nonlinear equation, combines both certainty and uncertainty in an equation from the point of view of dialectical logic. In geographic research, scholars usually transform non-remote sensing data into images and then generalize the remote sensing information model to the geographical image information model. Here, we take any data that can be portrayed as images into account and apply the model further to any field that is characteristic of complexity and non-linearity as geography. Then we obtain a general information model. Based on the analysis in terms of the formal logic principle, (Table 1) gives the analysis of the remote sensing information model and the general information model on intension and extension of certainty and uncertainty [19]. In logic, intension is the set of attributes constituting the meaning of a term [20].
It is often contrasted with extension, which is the class of objects to which the term applies. For a particular research subject, intension indicates all parameters that affect the results, and extension indicates the set of objects that the subject refers to. As Table 1 shows, when both intension and extension are certain, the studied phenomenon can be considered as a white system and it can be solved by using Mathematics- Physics equations. When both intension and extension are uncertain, the studied phenomenon can be considered as a black system and it can be solved by using stochastic equations. When intension is certain and extension is uncertain, the studied phenomenon is the transition of two certain phenomena, it can be considered as a fuzzy system and can be solved by using fuzzy equations. When intension is uncertain and extension is certain, the studied phenomenon is known incompletely, it can be considered as a grey system and can be solved by using grey equations. According to complexity of studied phenomena, a multifactor function y influencing phenomena can be expressed as [19].
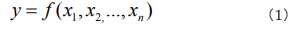
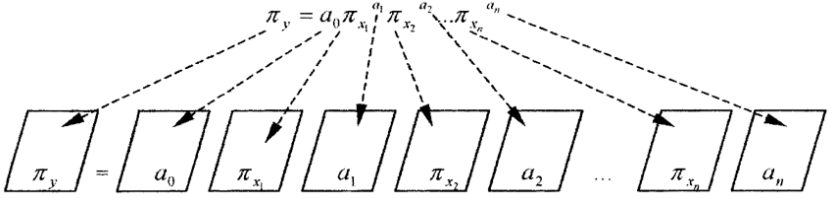
where x1, x2...,xn are n influencing factors. By doing dimensional analysis on y, x1, x2...,xn and applying the generalized π theorem which breaks the limitation of centimeter-gram-second system and gives the similar descriptions of all relative kinds of phenomena, one can attain the similar rules πy, πx1, πx2...,πxn [19]. Writing the similar rules as a general non-linear expression, one can generally obtain [19]
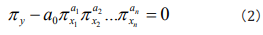
where πy is a non-dimensional factor group of the seeking phenomena, in which factors may have definite physical, ecological, environmental, genetic etc significances, respectively, for different studied phenomena. In Eq. (2), we call a0 as information coefficient and a1,a2,... an as information exponents. To find out the information coefficient and information exponents, one can rewrite Eq. (2) as a logarithmic equation [19]
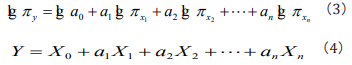
It is easy to see that Eq. (4) is a general multiple regression equation, one can solve the equation to obtain the value of X0 , a1,a2,... an and solve X0 = lg a0 to obtain the value of a0. When both the two sides of Eq. (3) equate to 1, it is easy to see that a1,a2,... an means the weight, the belonging degree in fuzzy mathematics [19].
In Eq. (2), such non-dimensional factor groups ( πxi ) are some similar rules in white system resulting from causal analysis, which satisfies quantitative causal relation [21-23], e.g. Ref.[24] uses the no-loss-no-gain homeomorphic map transformation satisfying the quantitative causal relation to gain exact strain tensor formulas in Weitzenböck manifold. In fact, some changes (causes) of some quantities in Eq. (2) must result in the relative some changes (results) of the other quantities in Eq. (2), so that Eq. (2)’s right side keeps no-loss-no-gain, i.e., zero, namely, Eq. (2) also satisfies the quantitative causal relation. The ellipses in Eqs. (2-4) mean the factors which have not been included in the equations for the lack of actual measured data or having not been recognized [19]. Thus, Eq. (2) leaves room for improving description on studied phenomena. With further research, some new similar rules might be found and then they can be added into the general information model [19]. Before finding the new similar rules, they are included in the information coefficient phenomenologically. The analysis of the information exponents suggests that:
(1) when ai (i =1,2,⋅⋅⋅, n) = 0 i there is no relation between 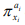 and πy; (2) when ai (i =1,2,⋅⋅⋅, n) = 1, there is a linear relation
between
and πy; (2) when ai (i =1,2,⋅⋅⋅, n) = 1, there is a linear relation
between 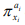 and πy; (3) when
and πy; (3) when 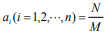 (fraction), there
is a fractal self-similar relation between
(fraction), there
is a fractal self-similar relation between 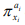 and πy; (4) when
and πy; (4) when 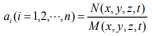 , there is a general space-time relation
between
, there is a general space-time relation
between 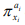 and πy [19]. From the above review, it is easy to
see that both the completely determinative physical equations
and the completely indeterminate stochastic equations are
special cases of Eq. (2). Both the certainty and the uncertainty are
combined in this grey non-linear equation, in which each similar
rule, the information coefficient and each information exponent
can be depicted as images. So, the general information model is a
dialectical logic calculation combining abstract thinking with visual
thinking as Figure 1 shows [19].
and πy [19]. From the above review, it is easy to
see that both the completely determinative physical equations
and the completely indeterminate stochastic equations are
special cases of Eq. (2). Both the certainty and the uncertainty are
combined in this grey non-linear equation, in which each similar
rule, the information coefficient and each information exponent
can be depicted as images. So, the general information model is a
dialectical logic calculation combining abstract thinking with visual
thinking as Figure 1 shows [19].
Four Kinds of Information Calculation Methods of DNA in terms of the General Information Model
As long as we find the similar rules of different information quantities according to their significances of informatics, we can achieve their particular equations by using the general information model. In this section, we deduce four kinds of information quantity equations usually applied in the DNA sequence research.
The nucleic acid sequence can be regarded as a linear text composed by four vocabularies—A (adenine), C (cytosine), G (guanine), T (thymine). A segment of length k (3~9) of nucleic acid sequence is called as a k-tuple [15]. There are 4k kinds of k-tuples and we can count the frequency (of occurrence) of each k-tuple by moving the window of length k with step length 1 along a DNA sequence [15]. It may be conjectured that the distribution of k-tuples in a genome would be the “equivalent representation” of the genome when k is big enough, namely, the genome sequence can be determined by the distribution of k-tuples uniquely [7].
Shannon’s Entropy in Word Domain
There are 4k kinds of k-tuples for a certain k. For example, when
k = 2, there are 16 kinds of 2-tuples (AA, AC, AG, AT, CA, CC, CG, CT,
GA, GC, GG, GT, TA, TC, TG, TT). We use i f to denote the frequency
of the i th kind of k-tuple and N to denote the total frequency of
k-tuples, determined by the equation: N= the length of the genome
sequence – k + 1. Considering the similar rules as the probability of
the frequency i f of each k-tuple, we attain 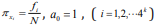 where the minus is due to
where the minus is due to 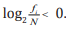 Then Eq. (3) can be embodied
as following:
Then Eq. (3) can be embodied
as following:
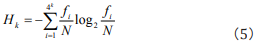
This is just Shannon’s entropy equation and is the same as the result in Ref. [15]. Therefore, we first discover that Shannon’s entropy is a kind of description on the combination of some different similar rules with respective weights.
Logarithm of Rate of Standard Deviation and Mean value in word domain ( logDTM )
Considering the quantity of A+T in a k-tuple, we can divide
the k-tuple into k+1 subsets, each of which called the m th subset
[15]. For example, when k = 2, there are 3 subsets: (1) m = 0, there
are four 2-tuples including neither A nor T—CC, CG, GC, GG; (2) m
=1, there are eight 2-tuples including one A or T; (3) m =2, there
are four 2-tuples only including A or T. We use Lkm to denote the
length of the m th subset for a certain k and fkm to denote the
average frequency of all k-tuples for a certain k in the m th subset
[15]. The corresponding standard deviation is 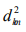 [15]. Regarding
the similar rules as the contribution of the standard deviation
[15]. Regarding
the similar rules as the contribution of the standard deviation 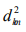 to the average frequency fkm of each m th subset, we obtain that
to the average frequency fkm of each m th subset, we obtain that 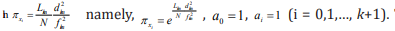 Then
Eq. (3) can be embodied as
Then
Eq. (3) can be embodied as
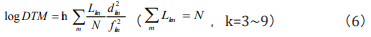
This is the log DTM equation, and is the same as the result in Ref. [15]. It could be proved that log DTM is related to Shannon’s entropy.
Shannon’s Entropy in Frequency Domain
We use mi
to denote the number of k-tuples occurring in a
certain interval and T to denote the number of intervals: T = the
total sequence length / the interval length. Considering the similar
rules as the probability of the number of k-tuples occurring in
different intervals mi
, we gain that 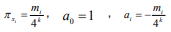 (i= 1,2,,...,T). Then Eq. (3) can be incorporated as
(i= 1,2,,...,T). Then Eq. (3) can be incorporated as
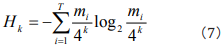
This is Shannon’s entropy equation in frequency domain, and is the same as the result in Ref. [15].
Fisher Information Quantity in Frequency Domain
So far, Fisher information quantity equation used in research on DNA sequence was defined directly according to its formal definition in statistics. We deduce the result firstly. As Fisher information quantity is defined
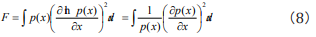
we discretize Eq. (8) to
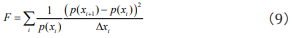
We may take 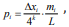 which represents the probability of the
number of k-tuple occurrence mi when the total interval length L
changed by ∆xi . Then Eq. (9) can be rewritten as
which represents the probability of the
number of k-tuple occurrence mi when the total interval length L
changed by ∆xi . Then Eq. (9) can be rewritten as
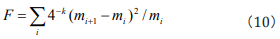
This is Fisher information quantity equation in frequency
domain and is the same as the result in Ref. [15]. Thus, we complete
the deduction of the Fisher information equation in terms of DNA
research from its formal definition. Considering the similar rules
as the distribution of k-tuples in different intervals measured
by Fisher information quantity in frequency domain, we get that  ai =1 (i=0,1,,....,4k). Then Eq. (3) can be embodied as Eq. (10).
ai =1 (i=0,1,,....,4k). Then Eq. (3) can be embodied as Eq. (10).
Based on above discussion, it is easy to see that the general information model is the uniform expression of different information measurements. Such uniform expression is not merely the combination of four equations but a model that reveals the essence of information quantity-the measurement of similar rules of systems. Put it clearly, Shannon’s entropy is the measurement of frequency occurrence of different k-tuples in word domain; log DTM is the measurement of the deviation of k-tuples frequency to mean value in different m th subset; Shannon’s entropy in frequency domain is the measurement of the number of k-tuples occurring in different intervals in global measurement; Fisher information in frequency domain is the measurement of the distribution of k-tuples occurring in different intervals in local measurement. On the ground of the correspondence of different similar rules to their information measurements, we can achieve the respective equations.
Application of the General Information Model to DNA Identification
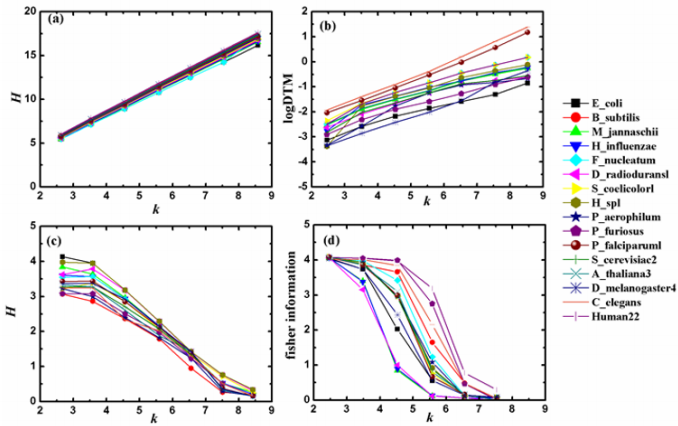
In research of living organisms, humans understand the macrocosm more concretely and amply than they know the microcosm. The general information model (which integrates deduction, induction and analogy into a whole and is characterized with image calculating function) can satisfy the demand of the status of modern research well and is helpful to the identification and analysis of DNA sequences. Ref. [15] shows the statistical results of the four information quantities calculated by Eqs. (5), (6), (7) and (10). The four information quantities are denoted by H(1) , H(2) , H(3) and H(4) , respectively. The relations between the four kinds of information quantities and the k-tuple word length k of DNA sequences of 16 typical genomes are displayed in Figure 2 [15].
Figure 2: The relations between four kinds of information quantities and the word length k.
(a) H(1) versus k (b) H(2) versus k (c) H(3) versus k (d) H(4) versus k
According to the results shown in Figure 2 (a-c), it is easy to find that the three Shannon’s information quantities have good linear relation with k (For the relation between log DTM and Shannon’s entropy, log DTM can be seen as a kind of Shannon’s entropies). Moreover, such linear relation is universal for different species on the whole. Shannon’s entropy is the measurement of uncertainty about a stochastic variable. It only depends on the certain probability distribution of the stochastic variable rather than its value. In the perspective of the general information model, similar rules of different information quantities are relative to the probability distribution of their respective stochastic variables, and the corresponding information exponents describe the weight each similar rule contributes. The above graphs show that the linear relation between H(1) and k is the most strong among the all. For H(1) = ak + b , the regression coefficient a is close to 2 and the interception b is close to 0. For a random sequence with infinite length, H(1) 2k = [7]. This suggests that H(1) of different species is close to that of random sequences; namely, their corresponding similar rules, information coefficients and information exponents are close to those of the random sequences. Actually, the neutral mutation causes all DNA sequences of different species close to random ones [16]. Thus, the similar rules, information coefficients and information exponents of them are alike, so the relation between H(1) and k shows the universality which is nearly independent of species.
As Figure 2d shows, the relation between Fisher information (4) H and k varies with different species, the level of linearity of which is heterogeneous with Shannon’s entropy. The reason is that the two measure information by using different methods in different measurements. The heterogeneity between their corresponding similar rules and information exponents results in the difference of relation between information quantities and k. For other two information quantities, the forms of their equations are different with Shannon’s entropy though, the three are defined by the same measurement method, i.e., the measurement of uncertainty about a stochastic variable associated with a certain probability distribution. Therefore, their similar rules and information exponents have commonness to some extent which may explain the similar linear relation.
Summary and Conclusion
This paper generalizes the concept of geographical remote sensing information model and extends it to a general information model. This grey non-linear equation has many advantages to the application in molecular biological research which contains both certainty and uncertainty associated with a myriad of data that may be described in images. We deduce the Fisher information equation in DNA domain from its formal definition. Then we obtain the equations of four kinds of information quantities in terms of DNA research by using the general information model and find that all kinds of information quantities we discussed are measurements of the similar rules of systems. The contribution of each similar rule to the whole system can be described in the form as the ai th power of π xi and ai can be considered as the weight.
The statistical data and graphs of 16 typical genomes cited from Ref. [15] show that three kinds of Shannon’s information quantities (Shannon’s entropy in word domain and in frequency domain and log DTM) have good linear relation between them and k but Fisher information has not. We explain the results from a new perspective the different statistical results are the manifestation of the heterogeneity between similar rules of Shannon’s entropy and those of Fisher information, which results from the difference between measurements of the two when people describe the smoothness of their probability functions p(X). On the other hand, the universality of the linear relation between Shannon’s entropy and k suggests that the more the similar rules, information coefficients and information exponents of different systems are similar, the more their characters and qualities are similar. Such universality also demonstrates that the general information model is an effective and advantageous way to analyze these problems regarding DNA research.
For more Articles on : https://biomedres01.blogspot.com/

No comments:
Post a Comment
Note: Only a member of this blog may post a comment.