A Maximum Cut Approximation Algorithm for Tracheostomy

Introduction
The MAX-CUT problem is one of the basic and most prominent problems in Approximation Algorithms, due mainly to its large connection with other optimization problems and their application in different domains, such as Data Mining, Critical Resource Allocation, among others. A graph G with vertex set V, and edge set E is given, and we want to partition it, in such a way that there should be the maximum number of edges between some set of vertices S and its complement V – S. Based on recent studies of randomized trail [1], it is considered necessary to wait for 10 days before a patient should be considered for mechanical ventilation. Since, complications are related to tracheostomies, such as: pneumothorax, bleeding, vocal cord dysfunction, etc., the performance of the surgery, and the selection of ill patients suitable for it, has been a relevant topic of debate.

Methods
The MAX-CUT problem is suitable for a single or multicommodity flow problem, where the underlying network has n nodes set V and m edges set E. Since each edge e is provided with a capacity flow C(e), such that a maximum nonnegative flow of C units can slip through the edge. Two particular nodes characterize the net, one is the source s and the other the sink t. The maximum flow that can run through it, from the source to sink, in accordance with the capacity restrictions is associated with the minimum cut, that is the subset of edges that need to be removed from the network, in order to disconnect the source s from the sink t. However, an interesting approximation to build a MAX-CUT from there is based on the greedy algorithm of local improvement. 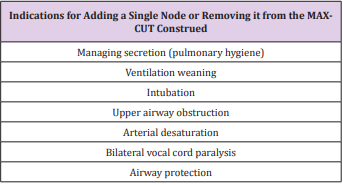Approximation algorithms for MAX-CUT are extensively studied in the literature [2], however the dynamic approach for our case is based on the sense of the capacities, based on the following indications shown in Table 1 [3-5]. 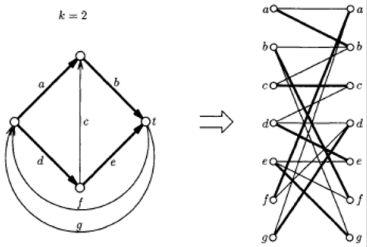The procedure is based on the following iterative cycle: Repeat Add a single node to the subset S, until no further improvement is possible (Figure 1).

Table 1: Criteria for the selection of patients for Tracheostomy.

Figure 1: Heuristic approach for the local improvement of MAX-CUT.

Discussion
Any search problem can be modeled as a relation of some function to the vertices of the {0,1}-cube of k- dimensions. In the case when all commodities between any two given edges are equal, the MAX-CUT is obtained by the conditions on the flow of the dual graph. 

For more Articles on : https://biomedres01.blogspot.com/