Oscillatory Diffusion and Chemical Vortices in Multicomponent Plasma

Introduction

Often laboratory and astrophysical plasmas are multicomponent, and diffusion of elements is important for some phenomena. For instance, diffusion processes can lead to chemical inhomogeneities and, as a result, to change the emission, heat transport, and conductivity [1-3]. In thermonuclear fusion, the source of impurities is usually the chamber walls, and diffusion determines the distribution impurities [4-6]. Even a small number of heavy ions influences the rate of radiative losses in plasma and changes its thermal properties. In astrophysical conditions, chemical inhomogeneities have been detected in the surface layers of many stars of various spectral types. It is widely accepted that these inhomogeneities are determined by diffusion processes but, however, the mechanisms resulting information of chemical spots is still uncertain. Diffusion in plasma can differ qualitatively from that in neutral gases because of the presence of charged particles - electrons. This particularly concerns hydrogen plasma [7]. In such plasma, the influence of electrons on diffusion of heavy ions is especially pronounced.
Chemical inhomogeneities can appear because of various reasons, for instance, it is often thought that chemical spots occur due to the presence of magnetic fields. The magnetic field B can magnetize electrons and produce a non-uniform distribution of ions. Anisotropy of transport is characterized by the Hall parameter, xe =ωBeτ where 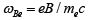is the gyrofrequency of electrons and τe is their relaxation time. 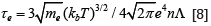In hydrogen plasma, where n and T are the number density and temperature of electrons, respectively, L is the Coulomb logarithm. The current-driven diffusion can lead to a formation of chemical inhomogeneities like other diffusion processes. Using a simple model, we show that the interaction of the current and field with impurities leads to their diffusion in the direction perpendicular to both. This type of diffusion can contribute to formation of chemical spots even in a relatively weak magnetic field with xe << 1. We also show that such diffusion can be accompanied by a particular type of waves in which only the impurity number density oscillates.

Formulation of the Problem and Basic Equations

Consider a cylindrical magnetic configuration with the field in a z-direction, 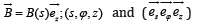are cylindrical coordinates and the corresponding unit vectors. Then, the electric current is given by

If jϕ → 0 at large s then B→ B0 =const at s→∞. Note that such magnetic configurations can be unstable for some dependences B(s) [9-11] but we assume that the instability does not occur for chosen dependencies B(s). Plasma is assumed to be fully ionized and consists of electrons e, protons p, and small amount of heavy ions i. A small admixture of heavy ions does not influence the dynamics of a background hydrogen plasma and these ions can be considered as test particles. The partial momentum equations in ionized plasma have been discussed by [7,12]. The paper [12] considers transport processes in the hydrogen-helium plasma but the derived equations describe the hydrogen plasma with a small admixture of heavy test ions. Then, the partial momentum equation for ions i has the form

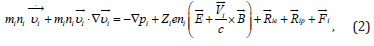
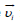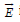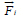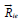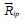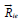where is the velocity, Zi is the charge of the species i, pi and ni are the partial pressure and number density, respectively, and is the electric field; is the external force on species i. We neglect the external force in our model since its influence is often insignificant. The forces and are caused by the interaction of ions i with electrons and protons, respectively. The forces and 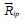are internal and their sum over all components is zero.

The velocity 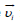can be represented as a sum of and 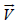where is the hydrodynamic velocity of plasma and ~V i is a diffusive velocity of ions i relative plasma. Since in our model ni is small compared to np, the hydrodynamic velocity is approximately equal to the mean velocity of protons, 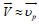. In this paper, we assume that background plasma is in hydrostatic equilibrium. Then, 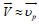= 0 and, hence, 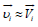. If the temperature is uniform, the friction force 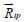has only a component proportional to the relative velocity of ions i and protons, 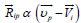. This force can be easily calculated if Ai = mi /mp >>1. Since the velocity of a background plasma is zero, 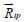can be represented as

[12], where 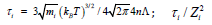is the characteristic time of scattering between protons and heavy ions; L is assumed to be the same for all types of scattering.

The friction force on the l.h.s of Eq. (2), 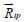, can be estimated as 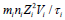and the first term in this equation is where Dt is the timescale of diffusion processes. Therefore, this term is much smaller than the friction force 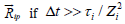. The second term on the l.h.s. of Eq. (2) is of the order of 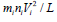where L is the characteristic length scale. Since L ~ Vi Δt , this term can also be neglected if 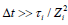. Then, Eq. (2) transforms into

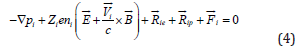
If ni << np , then, 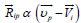is given by 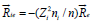[12], where 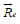is the force acting on the electrons. Since ni<< n, 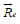is determined by scattering of electrons on protons but scattering of electrons on heavy ions gives a small contribution. Therefore, one can use for 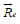the expression obtained by [7] for one-component plasma. In the case of a cylindrical isothermal configuration, this force reads

where 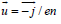is the velocity of electric current; 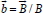; coefficients α ⊥ and α ∧ have been calculated by Braginskii [7]. The force (5) is caused a friction due to a relative motion of the electron and proton gases. Then, Eq.(1) yields for the current velocity

Consider the current-driven diffusion in a magnetic field with xe <<1 . Substituting 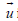into Eq.(5) and using coefficients α ⊥, ∧ we obtain with the accuracy in linear terms in xe

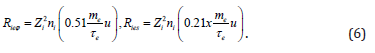
The momentum equation for the species i (Eq.(4)) depends on s E and Eϕ components of the electric field. The momentum equations for e and p, containing these electric fields, read

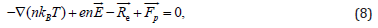
Using Eq. (5), we obtain

Substituting Eqs.(6), (3), and (9) into the s- and ϕ -components of Eq.(4), we arrive to the expression for a diffusion velocity, ,

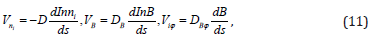
Vni is the standard diffusion velocity and VB is the velocity of diffusion caused by the current. The corresponding diffusion coefficients are

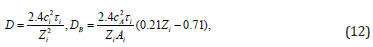
where .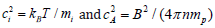

Distribution of Ions Under the Influence of Electric Currents

The condition of hydrostatic equilibrium reads in our model

where p and r are the total pressure and density of plasma, respectively. In hydrogen plasma, we have p ≈ 2nkB T where kB is the Boltzmann constant. Integrating Eq. (14) and assuming the temperature to be constant, we obtain

where 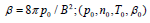are the values of (p, n, T, b) at s → ∞.

Consider the distribution of elements in equilibrium. Since Vis = 0 in equilibrium, Eq.(10) yields

The r.h.s. is responsible for the influence of currents on the distribution of impurities. One has from Eq. (16)

Taking into account Eq. (16) and integrating Eq.(17), we have

where μ = − 2Zi (0.21Zi− 0.71) and ni0 is ni at s →∞. If the local abundance of i is γi = ni/ n , then taking into account Eq. (17), obtain

where γi0 = ni0 /n Local abundances depend essentially on the field strength. These dependences are particular sensitive to B in the case of heavy ions with large charge numbers. If other diffusion mechanisms are negligible, then the exponent (μ − 1) reaches large negative values for large Zi and, as a result, strong abundance anormalies can be produced in this case. For instance, (μ − 1) is equal 1.16, -0.52, and -2.04 for Zi =2, 3, and 4, respectively. Note that (μ − 1) changes its sign with an increase of Zi : (μ − 1) > 0 if Zi = 2 but (μ − 1) < 0 for Zi ≥ 3. Therefore, elements with Zi ≥ 3 are in deficit (γi <γi0 ) in the region with a weak magnetic field (B < B0) but these elements should be overabundant in the region with a stronger field, B > B0.

Eq. (20) describes the distribution of impurities in diffusive equilibrium. The characteristic timescale to reach this equilibrium, tB, can be estimated as

where L is the length scale of the magnetic field, L = |d In B/ds|-1 . The characteristic timescale of baro-diffusion is given by the wellknown expression

Hence, the current-driven diffusion operates on a shorter timescale if DB > D or

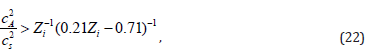
where cs is the sound speed, 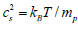. Therefore, the current-driven diffusion is more efficient if the magnetic pressure exceeds the gas pressure.

Chemical Vortices

In our simplified model of cylindrical magnetic configuration and velocity (10), the continuity equation for ions i has the form

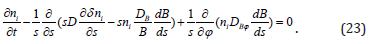
Consider the behaviour of small perturbations of ni by making use of a linear analysis of Eq. (23). In the unperturbed state, we assume that plasma is in a diffusive equilibrium and, therefore„ the unperturbed impurity number density satisfies Eq. (18). For the sake of simplicity, we assume that small perturnations are independent of z. Denoting disturbances of the impurity number density by i δ n and linearizing Eq.(23), we obtain the equation that describes the evolution of such small perturbations,

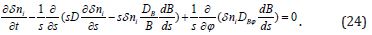
Consider only disturbances with a short radial wavelength. If this wavelength is shorter than the length scale of unperturbed quantities, then we can use the so-called local approximation. Then small disturbances are α exp(−iks)where k is the radial wavevector, ks >>1. Since the basic state does not depend on time and ϕ , perturbations can be represented in the form where m is the azimuthal wavenumber and ω should be calculated from the dispersion equation. Such disturbances have a shape of cylindrical vortices of a chemical composition. Substituting i δ n into Eq. (24), we derive the dispersion equation for such perturbations in the form

This dispersion equation describes a special type of magnetohydrodynamic waves where only the number density of impurities oscillates. Note that there are many different sorts of waves in magnetized plasma that can produce oscillations of a chemical composition. Such oscillations, for example, can be generated by standard magnetohydrodynamic waves [12] but, usually, fluctuations of impurities in such waves are accompanied by fluctuations of other hydrodynamic quantities. Indeed, the electric field has actively to take part in such waves and interact more efficiently with heavily charged ions than with protons. As a result, MHD waves can produce fluctuations of a chemical composition. However, these fluctuations are typically very small because the period of MHD waves is much shorter than the diffusion timescale. Chemical fluctuations become significant only if the period of a wave is comparable to the diffusion timescale.
The waves considered in this paper are caused by diffusion processes and their period is generally comparable to the diffusion timescale. Therefore, fluctuations of a chemical composition can reach a significant value in such waves. The quantity ωR is responsible for decay of these waves with the timescale 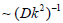typical for standard diffusion. The frequencies ωI and ωH describe oscillations of the impurities caused by the combined action of electric current and the Hall effect. The considered waves are oscillatory if | ωI + ωH|> ωR. The latter condition is equivalent to

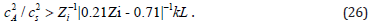
Therefore, the waves are oscillatory if the magnetic pressure is substantially greater than the gas pressure. The frequency of diffusion waves is higher in the region where the magnetic field has strong gradients. The order of estimate of ωI is

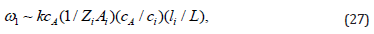
Where li = ciτi Note that different impurities in such waves oscillate with different frequencies.

Conclusion

Diffusion of heavy ions in plasma under the influence of the current-driven mechanism has a number of features. Generally, the diffusion velocity can be comparable to (or even greater than) that caused by other diffusion mechanisms. The currentdriven mechanism can lead to a formation of chemical spot even if the magnetic field is relatively weak. Note that other diffusion mechanisms usually require a much stronger magnetic field. The current-driven 83 diffusion is caused by the Hall effect and electric current and, therefore, it leads to diffusion of heavy ions in the direction perpendicular to both the magnetic field and current. Therefore, a distribution of elements is determined by a geometry of the magnetic fields and electric currents. Chemical inhomogeneities can manifest themself, for instance, by a nonuniform distribution of plasma temperature and emission. Note that this type of diffusion can be important also in some conductive fluids if the magnetic field is sufficiently strong. Our consideration shows that a special type of magnetohydrodynamic waves may exist in multicomponent plasma.

These waves can be periodic if the magnetic field is sufficiently strong, and they are characterized by oscillations of the impurity number density alone. The frequency of such waves is rather low and is determined by a characteristic diffusion time. The order of magnitude estimates of this frequency yields 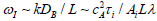Lλ where λ = 2π / k is the wavelength. In stellar conditions, such waves can manifest themselves in pecular magnetic stars where the magnetic field is ∼ 104 G and the number density and temperature are ∼ 1014 cm−3 and ∼ 104 K, respectively. If the length scale, L, and λ are of the same order of magnitude (for instance, ∼ 1011 cm), then the period of such compositional waves is ∼ 3 × 103 yrs. This is much shorter than the magnetic timescale and generation of such waves should lead to short-term spectral variability. Such waves can exist in laboratory plasmas as well, but their frequency is much higher in this case. If B ∼ 105 G, n ∼ 1015 cm−3, T ∼ 106K, and L ∼ l ∼ 102 cm, then the period of compositional waves is ∼ 10−8 s. Note that frequencies of waves with various impurities can differ essentially since they depend on the sort of heavy ions.

In terrestrial conditions, the compositional waves also can manifest themselves by oscillations in spectra. In astrophysical conditions, the magnetic field has usually more complex topology than that considered in our model. In some cases, however, cylindrical magnetic configurations can mimic the magnetic field in certain regions. For example, the field near the magnetic poles in stars has approximately cylindrical symmetry [13] and our results describe qualitatively diffusion in the region near the poles. Therefore, the current-driven mechanism in combination with other diffusion processes contributes to a formation of chemical spots in various types of stars. For example, this mechanism can contribute to formation of element spots in Ap-stars where the magnetic fields have been detected. Also, many neutron stars have strong magnetic fields and topology of these fields is rather complex with spot-like structures at the surface. Such magnetic configurations can be responsible for formation of a spot-like chemical distribution at the surface. For example, evolution of neutron stars is very complicated, particularly, in binary systems [14] and, therefore, their surface chemistry can be complicated as well. Diffusion processes may play an important role in this chemistry.

For more Articles on : https://biomedres01.blogspot.com/