An Elastic Finite Element Analysis of the C2-C7 Human Cervical Spine Segment

 

Introduction

The human spine is a complex structure that supports the weight of the body, transfer loads from the head and trunk to the pelvis and protects the spinal cord [1]. Due to its complex anatomy and flexibility, the segment of the spine most likely to be injured is the cervical spine. Cervical injury can be a result of extension, flexion, contusion, compression and rotation of the spinal cord. Traumatic accidents such as motor vehicle, sports, falls, overloading, etc., are the most frequent causes of cervical injuries. No traumatic cervical injury causes are arthritis, cancer, compression fractures from osteoporosis, and inflammation of the spinal cord [2]. Therefore, it is necessary to fully understand the biomechanical response of the cervical spine to external stimuli (injury and dysfunction). Biomechanical finite element models facilitate the understanding of the mechanisms of dysfunction, spinal injury, and spinal responses to various clinical problems and treatments. In earlier cervical spine models developed to predict only spinal motion or displacement response to loading, the vertebrae are simulated as simple rigid bodies, while other connective tissues are represented as beams, truss or spring elements.

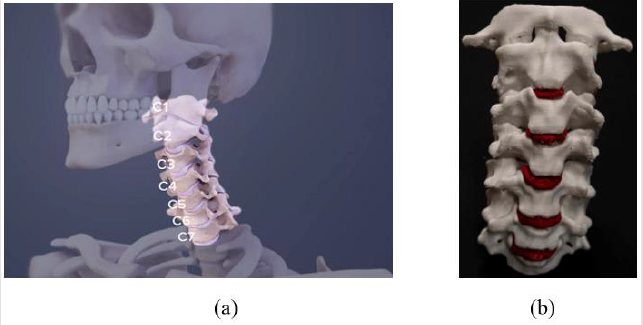
Actually, anatomically precise 3D-FE models are being widely adopted to evaluate stresses, strains, displacements and rotations in complex spinal vertebrae, facet joints, ligaments, and soft tissues. The present study was carried out to illustrate the goodness of the finite element method as it can provide general information on spinal behavior (response) to external stimuli. The symbols for the upper 7 cervical vertebrae (C1 through C7) are shown on Figure 1a. Each of these seven vertebrae in the neck has a predetermined function, creating very specific problems when they are not aligned. Located at the top of the neck and base of the skull, the C1 vertebra is the first cervical vertebrae in the entire spine. Called atlas and shaped like a ring, this vertebra supports the head and allows it to rotate. It is held in place by muscles, and is secured by a thick and strong ligament called the transverse ligament. This bone is named the Holy Grail of the human spine, and misalignment at this joint can cause troubles for the entire body [3].

The first cervical vertebrae rotates around the dens (the superior protruding long bony element from the C2 vertebra), allowing the head to turn in different directions. The C2 vertebra, also called the Axis, is a hinge that makes the C1 vertebra pivot with the consequent turn of the head. When the C2 vertebra becomes subluxated (a misalignment in the axis vertebra), it can result in pain, difficulties to turn the head as well as creating specific secondary health issues related with sinuses, eyesight, hearing, head and even the tongue [4]. The joint Atlas (C1)-Axis (C2) is called the atlanto-axial joint. Unlike other vertebral joints, this special joint does not have an intervertebral disc. It is the most mobile section of the entire spine, and it is responsible for the 50% of the extension and flexion of the neck, and 50% of the rotation of the head [5]. In the present study, encastered boundary conditions were applied in the inferior surface of the C7 vertebra. Due to the length of its spinous process, this vertebra located at the base of the neck sometimes is called the prominent vertebra (Figure 1).

Figure 1:The human cervical spine

(a) Raw state of the model with skull C0

(b) The 7 stacked bones called vertebrae labeled C1 through C7 and the intervertebral discs in red color. The top and the bottom of the cervical spine connects to the skull and to the upper back at about shoulder level, respectively. A lordotic curve (curving toward the front of the body and then back) is gently formed in the spine.

Advancements in biomechanical finite element techniques (in terms of material properties, component modeling, and validation procedures) enabled investigators to propose more accurate models of the cervical spine system. Even though actual finite element models of the cervical spine consider more accurate representation of the geometry of vertebrae, intervertebral discs, facet joints, ligaments and spinal cord tissues, the FE modeling of the cervical spine unit as a whole is lack off. One of the reasons is that geometry definition of bone from CT scans involves the application of a specific meshing procedure. The integration of new technologies such as digitalized quantitative axial computed tomography (CT) scans, and STL-CAD methods used to generate FE closed volume geometry of the bone structure, allow to construct more accurate and comprehensive models, increasing efficiency and model applicability. At the present time, efforts are focused to better reproduce the complex geometry of the spine.

To reach the goal, digitalized quantitative axial computed tomography (CT) scans, and STL-CAD methods are being combined. Numerous commonly open source and proprietary-software programs are available for use with DICOM data sets. For instance, to generate the FE closed volume geometry of the bone structure, segmentation mask during image processing of medical CT data is currently conducted by using specialist software such as 3D Slicer [6] or Mimics [7], and the specific meshing procedure with software such as OsiriX [8] or MeshLab [9]. 3D Slicer is an open

source software platform for image informatics, medical image processing, and three-dimensional visualization. On the other hand, for processing and editing 3D triangular meshes, Mesh Lab is a powerful software that provides a set of tools for inspecting, editing, healing, cleaning, texturing, converting and rendering meshes. Features for preparing .STL models and for 3D printing processing raw data produced by 3D digitization tools/devices are also offered. STL is a file format native to the stereolithography CAD software widely used for rapid prototyping, 3D printing, and computer-aided manufacturing (CAM).

The Model

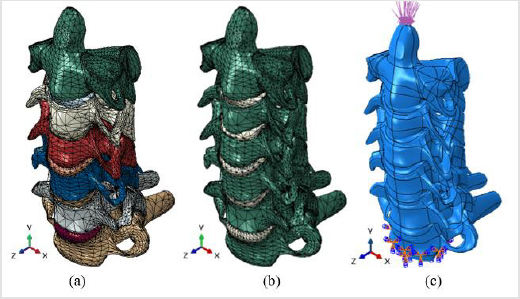
In this work, to construct the 3D-FE model, the cervical closed volume it was directly downloaded from the embodi3d web page [10]. The downloaded file was imported into the FE code ABAQUS [11] for creating an isotropic static finite element model. The model was significantly speeded up by using 76854 C3D10 tetrahedral solid elements and 132723 nodes. To assess the overall behavior of the C2-C7 spine segment in four different load modes (compression, lateral bending, flexion and extension), the model was statically loaded in four different surfaces of the superior projecting bony element from the second cervical vertebrae (i.e., the odontoid process, or dens). Encastered boundary conditions were used to fix translation and rotation in every node located on the inferior surface of the C7 vertebra. Other types of loading such as tension, shear, and axial rotation can be applied on other cervical spine locations (e.g., the superior aspect of the uppermost vertebra). Of the same manner, to simulate the skull and body weight, a follower load may be applied to each vertebra. An applied compressive vertical load and encastered boundary conditions are outlined in Figure 2c.

Due to the strong transverse ligament that secures the joint (the atlanto-axial joint) between the C1 and C2 vertebrae was not available in the downloaded file, the joint C1/transverse ligament/ C2 was excluded from the FE analysis, and the study was simplified to simulate the C2 through C7 unit. The assigned material properties (Young’s modulus for the vertebrae E=10000 MPa, Young’s modulus for the discs E=1000 MPa, and Poisson´s ratio ν = 0.3 for both groups) were considered in the whole analysis. Material properties were assumed to be homogeneous. The last because at the macro level, the material heterogeneities and defects can be assumed evenly distributed throughout the material sections and be represented by the assigned values. Continuous materials properties were assigned to the C2-C7 structure separating the vertebrae and discs in two different material groups (Figure 2b). Most simulation studies use homogeneous and isotropic material definition for the vertebrae and discs (Figure 2).

Figure 2:The C2-C7 human cervical spine segment

(a) The eleven parts (vertebrae and intervertebral discs)

(b) The two material groups

(c) An applied compressive vertical load and encastered boundary conditions.

The vertebrae and discs are generally modeled as a single linear elastic material. That is, the components of the vertebrae (cortical, cancellous, and posterior) and the components of the disc (nucleus and base of the annulus) are considered to form single materials but not composite materials. This assumption is clinically relevant to replicate disease or injury. As a first approach, in the present study, the entire vertebrae and discs were considered be isotropic single parts (single materials), so, they were not broken down into posterior elements, radial cortical shell, cancellous core, superior and inferior endplates, nucleus and annulus ground. During activities of daily living, it is estimated that the human cervical spine supports a compressive vertical load in the range of 120 to 1200 N [12]. However, ex vivo experiments show it buckles at approximately 10 N. As differences between the estimated in vivo loads and the ex vivo load-carrying capacity exist, in this work, a pressure distribution of 10 MPa was statically applied in four different surfaces of the odontoid process, or dens (See Figure 3). The application of a pressure load avoid the concentration of stress produced from point loads.

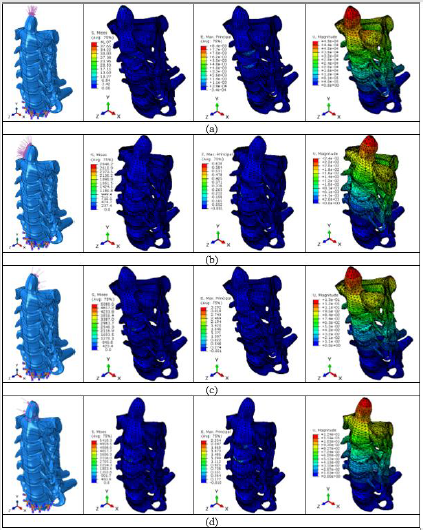
Figure 3:Mises stresses, maximun principal strains and displacements for the corresponding load modes (a) Compression; (b) Lateral bending; (c) Flexion; (d) Extension. The plotted Mises stresses and the displacements are in MPa and in mm respectively.

Results

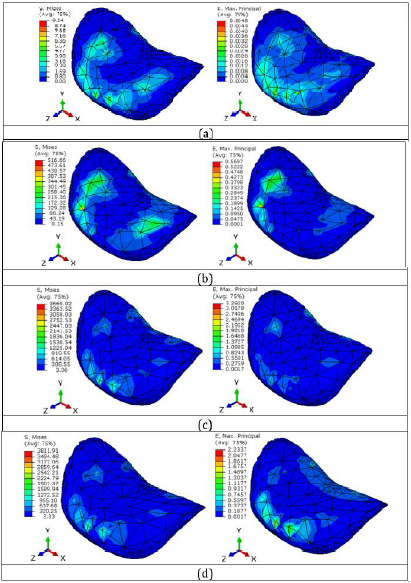
Figures 3 & 4 show ABAQUS finite element results in the multilevel cervical C2 through C7 unit shown on Figure 2. Magnitudes of von Mises stresses, maximun principal strains and displacements were recorded for each load mode. It is observed in Figure 3 that higher strain values develop in the flexion (bend forward) load mode, and higher stress values in the extension (bend backward) load mode. The stress and strain values collected in the upper face of the C3-C4 intervertebral disc are presented in Figure 4. It can be seen that the highest strain values reported for the flexion and extension modes in Figure 3 are located in the intervertebral disc shown. Also, it is observed that at a constant pressure distribution, the spine response to the compression load mode is much lower in two orders of magnitude than the spine response to the flexion, bending and extension load modes. Deformations in the compression mode do not result in strains that would cause the material to exceed the proportional limit; that is, the material remains within the elastic limits of Hooke’s law.

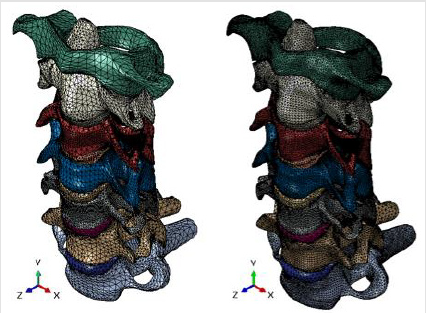
It appears that the stress concentrators (created in irregular shapes and related coarse meshes) and the type of load mode are responsible for the high stresses observed. Therefore, to test the sensibility of the FE mesh size in stress results, additional work has to be done by using fine mesh grids as those shown in Figure 5. Future modelling will be directed to simulate the C1-C7 segment incorporating the transverse ligament in the atlanto-axial C1-C2 joint.

Figure 4:Mises stress and maximun principal strain values collected in the upper face of the C3-C4 intervertebral disc (a) Compression mode; (b) Lateral bending mode; (c) Flexion mode; (d) Extension mode. Mises stresses in MPa.

Figure 5:Two finite element fine mesh grids of the C1-C7 human cervical spine segment. The twelve parts (vertebrae and intervertebral discs) are clearly identified.

Conclusion

a. A three-dimensional linear isotropic elastic FE analysis of six adjacent cervical vertebrae (C2-C7) has been developed. The model is composed of vertebrae and intervertebral discs.

b. A procedure for creating a finite element model based on available biomedical closed volumes obtained from CT scans was introduced.

c. It is observed that higher strain values develop in the flexion load mode, and higher stress values in the extension load mode.

d. It appears that the stress concentrators (created in irregular shapes and related coarse meshes) and the type of load mode are responsible for the high stresses observed.

e. It was found that at a constant pressure distribution, the spine response to the compression load mode is much lower in two orders of magnitude than the spine response to the flexion, bending and extension load modes.

f. The study was carried out to illustrate the goodness of the finite element method on spine biomechanics research.

For more Articles on : https://biomedres01.blogspot.com/