A Tensional Network in the Knee

The Medium of Haptic Perception

In contrast to the widespread assumption that the neural system generates impulses to the motor units in the skeletal muscle fibers, Turvey [1] place high importance on the fibrous collagenous connective tissues in the body; these are seen as providing a tensional network throughout the whole body, the biomechanical properties of which provide the framework for muscular force transmission as well as for the haptic sensory system. To identify the haptic system’s medium, Turvey focused on connective tissue and the conjunction of muscular, connective tissue net, and skeletal as the body’s proper characterization Turvey [1]. Myers has also posed the medium as a body-wide responsive physiological network—the myofascial meridian Myers [2]. Taking on ‘geometry’ first, cell biologist Donald Ingber placed one final piece of the puzzle: to view the body’s architecture in the light of ‘tensegrity’ geometry Ingber [3]. ‘Tensegrity’ was coined from the phrase’ tension integrity’ by the designer R. Buckminster Fuller (working from original structures developed by artist Kenneth Snelson Skelton [4]. As Snelson describes it Snelson [5], “The sculpture could be put into orbit in outer space, and it would maintain its form. Its forces are internally locked. These mechanical forces, compression, and tension or push and pull are invisible—just pure energy—in the same way that magnetic or electric fields are invisible.”
The tensegrity principle describes precisely the relationship between the connective tissues, the muscles, and the skeleton. For example, weight applied to shank/thigh bones would cause it to slide off its knee joint if it were not for the tensional balances that hold it in place and control its pivoting Swanson [6]. The invariant feature of tensegrity structures encompasses those that stabilize themselves through a phenomenon known as pre-stressing. Architects call this type of pre-stressed structural network, composed of opposing tension and compression elements that self-stabilize its shape by establishing a mechanical force balance, a tensegrity structure. Bio tensegrity is a term introduced by Dr. Stephen Levin and denotes the application of tensegrity’s principles to biological structures Hutson [7]. Tensional forces naturally transmit over the shortest distance between two points, so the elastic members of tensegrity structures are precisely positioned to withstand applied stress. For this reason, tensegrity structures offer a maximum amount of strength for any given amount of material Myers [2]. Furthermore, the invariant feature of a knee tensegrity system (specified by a given set of external forces such as the ground reaction force (GRF)) is a stable equilibrium if the structure returns to the initially given configuration after the application of arbitrarily small perturbations with respect to the functional knee axis (FKA) anywhere within the configuration Ingber [3].
Kim [8] showed how the knee tensegrity system manages the balance between tension and compression during locomotion by utilizing a unique combination of the FKA and GRF stimuli Kim [8]. When deformed by the shank to the ground via GRF, the strain is distributed over the whole structure, not locked into the joint itself by virtue of the assembly Phillips [9]. Thus, a reaction torque is zero on the knee joint if the GRF line of action intersects the joint axis. The configuration can exert a significant force on the ground without overloading the knee joint. This study aims to introduce the conception of the tensional network in muscles, i.e., the action lines that satisfy the given condition as the tensegrity’s structure is characterized by transmitting forces across the bones Kim [10]. Thus, we hypothesized that tensional forces in muscles are derivable from a scalar function, the work function.

N-lines as the Medium of Haptic Perception

Neurophysiologist Nikolai Bernstein (1967) defined coordination as mastering the many degrees of freedom (DOF) of a particular movement by reducing the number of variables to be controlled Turvey [11]. Recently, a contemporary perspective on Bernstein’s concept of synergies has been proposed Profeta [12]. The muscle synergy is equivalent to the complexity of lines, a manifold approximated by individual fibers Kim, et al. [13]. Muscles are not functional units, even though this is a common misconception. Instead, most muscular movements are generated by many individual motor units distributed over some portions of one muscle, plus portions of other muscles. The tensional forces of these motor units are then transmitted to a complex network of fascia sheets, bags, and strings, which convert them into the final joint/body movement Myers [14]. We define an n-line in a body as a member of the tensional network by virtue of some constraint upon the body Phillips [9]. This will mean that, whereas all n-lines in a body will immediately become a tensional network as soon as the body begins to move, not all members in a tensional network in a moving body will have been n-lines before they began to move. The whole regulus of n-lines is a tensional network for the three constraints at the instant (Figure 1a). This single infinity of n-lines are the generators of the regulars of lines, a linear ruled surface, upon the hyperboloid. Given any three lines in a body (protectively independent) which are bespoken by virtue of some existing constraints to be n-lines in the body, the whole regulus of lines to which the three bespoken lines belong are also n-lines in the body.
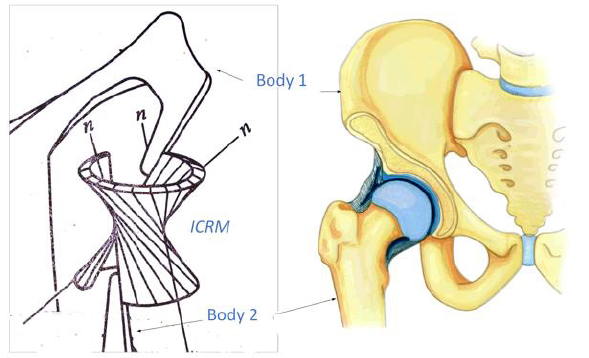
In (Figure 1), if any four forces along the n-lines are in equilibrium, their lines of action will reside in space as the lines of some regulus. What makes this remarkable is that, while any three of the lines of action are enough to define the hyperboloidal surface, the fourth line of action will be found, not to miss or to intersect that surface, but to lie automatically and exactly upon it. The object of the illustrated apparatus in (Figure 1) is to set up body 2 with 3 DOF with respect to body 1 in such a way that, within it, three n-lines do exist. The 3 DOF speaks about a body’s ICRM, its instantaneous capacity for relative motion with respect to some other body. It should next be clear that, given this infinity of n-lines in (Figure 1a), there is a corresponding infinity of hinges, which are the generators of the other regulus upon the same hyperboloid. The articulation between bones in (Figure 1b) is ball-and-socket type, which can take up the single infinity of hinges as the ICRM, which seem to be continuously registered by the joints; the changes of the angles seem to be episodically registered by their input to the nervous system Gibson [15]. The question to be answered is this: How does a perceiver feel what he is touching instead of the cutaneous impression and the bone posture as such Gibson [15]? Now to answer the question. In brief, The ICRM of the body (with its 3DOF) can be exactly reproduced by the substitution of (6DOF-3) direct points of contact between the body and its frame.

Figure 1:

(a) A regulus of n-lines represents the tensional network. It physically connects bodies 1 and 2. The whole regulus of hinges is an equivalent mechanical substitution for the three n-lines at the instant
(b) The articulation of bones is the ball-and-socket type.

Tensional Network

Skelton [16] defined a tensegrity configuration of rigid bodies as follows Skelton [16]. In the absence of external forces, let a set of rigid bodies in a specific configuration have torque less connections (e.g. via frictionless ball-joints). Then this configuration forms a tensegrity configuration if the given configuration can be stabilized by some set of internal tensile members, i.e. connected between the rigid bodies. The configuration is not a tensegrity configuration if no tensile members are required and/or no set of tensile members exist to stabilize the configuration. (p. 1) which are conjointly reciprocal to the ICRM as indicated by their intersections (at the ⊗ ’ s). A balance of forces happens when the virtual coefficient vanishes, being it the necessary and sufficient condition for knee equilibrium. The original anatomic schematics and lines of action were published previously Kim, et al. [17-19] and are used with the permission of Professor Michele Conconi. The video is available:
h t t p s : / / d r i v e . g o o g l e . c o m / f i l e / d / 1 8 _ Y t s z z T 3 _ IvNIken5uxObj4jmSd0Zs_/view?usp=sharing
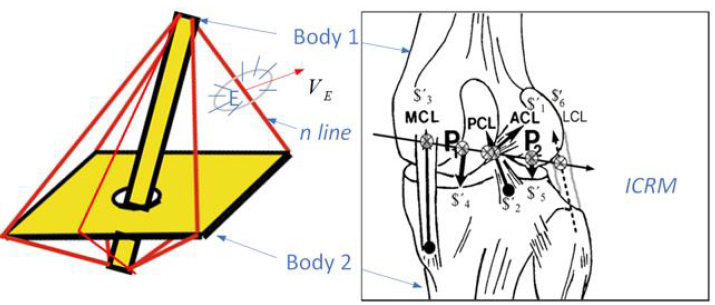
Attached to body member 1, in (Figure 2a), by mean of five taut strings, there are five n-lines, exhibiting a body with 1 DOF. It follows that body 2 suffers constrained motion as the tensegrity system moves that the paths in body 1 of all pints in body 2 are predetermined. (Figure 2a) is a stable embodiment of the same tensegrity configuration, hence a tensegrity system, exhibiting a torque less connection between body 1 and body 2. The line n-E-n in (Figure 2a) is an n-line by this definition, for it is a tensional network by virtue of a constraint. A member in the tensional network in a moving body is any straight line that joins two points in the body whose linear velocities are perpendicular to the line. The instantaneous velocity at point E,, is not yet known without analysis. Still, we know that it will occur in one or another of the directions indicated by the planar pencil of possible directions vectors drawn upon the flat surface perpendicular to the n-line at the point there, E (Figure 2a). The intra-articular structures of the tensegrity system of the knee include the muscles, the anterior cruciate ligament (ACL), posterior cruciate ligament (PCL), medial collateral ligament (MCL), lateral collateral ligament (LCL), and articular contact in the medial (P1) and lateral (P2) compartments (Figure 2b) Kim [18]. We have shown that six n-lines or constraints are members of the “tensional network” and are spatially oriented in such ways that by imposing an internal tension or “pre-stress” to reduce the play in the system; this ensures immediate mechanical responsiveness (all others feel, i.e., that movement of one element) and reduces impact fatigue at the joint.

Please refer to the authors ‘ previous works towards a visualization of the linear complex set Kim [13]. Let us look at the case next of six forces in equilibrium. When six forces are in equilibrium, their lines of action in the n-lines in the tensional network will be members of the same linear complex. Line manifold contraction is a linear line complex Jessop [20] defined by screws ICRM (Figure 2b). Using the superposition principle of infinitesimal quantities of DOF Kim [21], we can apply these two types of displacement as a body twist around a screw called Instantaneous Screw Ball [22]. The lines remain within the complex in any screw motion along a line axis, forming a linear complex. Additional cognitive processes or internal representations are not needed to explain these phenomena, as perception and action are coupled. Perceptual systems are active sets of organs designed to reach equilibrium through synergies Smart [23]. Our previous research Kim, et al. [24] introduced the concept of measurable invariance of the knee perceptual organ. In such invariant, six constraints ($) are collectively reciprocal to the instantaneous knee screw (ICRM) indicated by ⊗ (Figure 2b). These metrics predicted the knee synergy model based on synergies Turvey [25]. Moreover, this perspective defines torque-free pure forces based on the tensegrity structure Kim, et al. [26,27,21,24].
It is important to note that this configuration is a tensegrity configuration, as the system is pre-stress able in the absence of external forces, such as ground reaction forces during actual locomotion Skelton [16]. It was shown the knee tensional network (KTN) has six constraints and that it can balance the forces between tension and compression in the joint such that no work results Huang [28]. The KTN can be pre-stressed to obtain the same configuration as if external loads were applied. The selected pre-stress may yield the same configuration in the swing phase (external forces are absent) as in the stance phase (external forces are present) Skelton [9]. Notably, preparedness is not only a reactive aspect of the movement apparatus, but it also relates to anticipatory adjustments that predispose a system to behave in a particular way Profeta [12].

Figure 2:

(a) A set of rigid bodies in a specific tensegrity configuration have torque less connections.
(b) The knee joint synergy is represented by six constraints ($' , 1,..,6 i i = ).

Ensembles of a Geometric Pattern

It has been shown that a special kind of line in a body, which is determined by the constraints, namely n-line, is a regularly occurring and probably useful kind of line in bio tensegrity. Moreover, an important theorem about the overall layout or tensional network of n-lines in a body has been presented: the beginnings of a geometric pattern that emerged; it has been found in some special cases only, that associated 1 DOF and 3 DOF of a body in tensegrity, there are ensembles of n-lines existing which are, respectively, linear complex and regulus. This study has shown that the appearance or otherwise of n-lines in a body is a mystery. Still, it can be said that throughout the knee tensional network run two forces in the two types of n-lines: the one is mechanically operated by direct contact between bodies Lanczos [29]; the other is the living force exerted by the neuromuscular mechanism. Sylvester has shown that when six n-lines in (Figure 2) are so situated that forces acting along them equilibrate when applied to a free rigid body, a certain determinant vanishes, and he speaks of the six lines so related as being in involution Ball [22]. We shall see in a later investigation that these ensembles of lines figure largely and continuously in the theory of freedom and constraint of the tensegrity.

For more Articles on: https://biomedres01.blogspot.com/