Multiaxial Tensile Properties of Soft Biological Tissues

Short Communication

The results of virtual simulation of soft biological tissues often differ significantly from their real behaviour. Possible reason is that only data from unidirectional tensile test is considered. The aim is therefore to provide usable information on the mechanical behaviour of tissues under multiaxial loadings. The bulge test is the simplest way to realize biaxial tensile loadings on soft tissues. Several literature sources are critically examined and the known test specifications for the biaxial tensile test are significantly improved, see [1-5] among others. Our method supplies data for understanding human health and for reliable material modelling in adjustment of components for medical industries.

The implemented optical 3D measurement during the loading allows the precise capture of the mechanical response of the tissues until failure. The data from new test specification improves the material modelling thus providing the basis for an enhanced design quality in medical techniques and applications. The method was originally applied on elastomer sheets. In this way, parts for automobiles, components in aircraft construction or products for sports, medicine, and household can be designed more reliably and cost-effectively.

Mechanical Tests

Soft biological tissues obviously have some properties comparable to elastomers. The first standards on mechanical testing of elastomers date back to 1912 [6]. The state-of-theart recommendations are summarised in BS 903-5:2004 [7]. The characterization of elastomers occurs as experimental determination of the stress / strain relations. Often, only the measurements in tension are carried out according to ASTM D412 or DIN 53504:2017-03. Although the required material parameters can be determined from this test, the reliability of the material answer under multi-axial loadings is unsatisfactory.

For reliable material modelling, it is necessary to consider further measured data under shear and uniaxial compression.

Some testing standards for these tests like:

• Quadruple test according to ASTM D4014 and

• Compression test according to ASTM D395-18, D6049- 03, D6147-97, DIN ISO 815-1:2016, DIN ISO 7743:2016 are sometimes hard to apply to soft biological tissues. An alternative to the uniaxial compression test is the biaxial tensile test. Both tests describe the same deformation mode and, with the assumption of incompressibility, are convertible. The biaxial tensile loading on tissues can be implemented as bubble inflation test or bulge test. The disadvantage is that this test is not specified in any standard and provide results, which can often be arbitrarily interpreted. Large deviations in measurement series happen due to the different sample dimensions, ways of fixation, and test settings.

Bulge Test

The test setup consists of a base plate and a circular ring with an orifice (Figure 1). The tissue is clamped in the fixture and inflated with water, causing it to expand as a bubble. Stress singularities in the clamping area are reduced by a special design of the edges of the orifice. To ensure optimum fixation of the test specimen, the circular ring is centred and carefully bolted to the base plate. The protrusion of the specimen in the test area during clamping is minimised by design of the ring. A balanced biaxial stress occurs in the centre of the bubble during the loading (Figure 2). The ruler is used only for visual control of the height of the bubble. The evaluation of the geometry change in the bubble is performed in a subsequent post-processing step using the GOM Aramis 3D software. Alternative fluids like physiological saline solution can be used as a pressure medium. The tests can be performed according to customer specifications or our standard.

Figure 1: Inflated test specimen without black & white pattern, applying the orifice of the Ø50 mm diameter. Photo: Fraunhofer LBF.

Figure 2: Inflated test specimen without black & white pattern close to failure. Stress whitening can be observed. Photo: Fraunhofer LBF.

Specimen

Optimal results are obtained for specimens with an external diameter until Ø110 mm. The thickness of the materials is measured before the test at three positions. This measurement is based on a method developed at the Fraunhofer LBF, which avoids the induction of stress concentrations in the specimen. The specimen is speckled with a statistically distributed black & white pattern and then tested directly to ensure optimum adhesion between the specimen and pattern (Figure 3). This allows the evaluation of two- dimensional strains on the specimen surface by digital image correlation as function of pressure. To obtain data on possible anisotropy of the tissue, all specimens are mounted in the test fixture in the same position, considering their orientation when taken out. The setup allows the sample to be placed on the base plate without air bubbles, ensuring that the incompressibility assumption for the pressurized media is met.

Figure 3: Inflated test specimen with black & white pattern. A spot of Ø16 mm without pattern is left unpainted in the fourth quadrant of the specimen to study possible stress whitening during the loading. Photo: Fraunhofer LBF.

Evaluation of Three-Dimensional Deformation by Digital Image Correlation

The test results can be evaluated up to an approximate height of the bubble of 45 mm. Here, the maximum height is set by varying the diameter of the circular orifice. The inner diameter of the circular orifice of Ø40 to 50 mm is recommended for a test specimen (e.g., pleura or peritoneum) to obtain useful results in the evaluation. For thin tissues such as foetus vesicae, the diameter is reduced to Ø30 mm. An elliptical orifice can also be used to obtain additional stress states in the bubble for more in-depth material analysis.

Design engineers may be provided with the following data (Figure 4):

1. Time,

2. Pressure,

3. Height and curvature of bubble,

4. Principal strain,

5. Max. strain in x and y direction, and

6. Max. VON MISES equivalent strain.

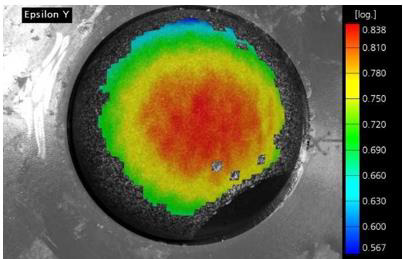
Figure 4: Results of the evaluation of the bulge test: logarithmic strain s𝑦𝑦 at maximum load. Photo: Fraunhofer LBF.

All experimental data are available as ASCII, .jpg, and .mov files.

Modelling

Soft biological tissues are often modeled as a perfect hyperelastic material. For 3D description, the existence of the strain-energy function W is assumed: the stress response can be determined from the applied deformations alone [5].

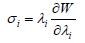
with 𝜆i – principal stretches and 𝜎i – principal stresses related to the undeformed condition.

The W-function is unknown. Different approaches are compared in [1,8-12] among others. The polynomial RIVLIN equation for hyperelastic material behaviour, postulated without material structure considerations

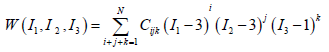
contains some known W-functions. It is formulated as function of the irreducible invariants of the left CAUCHY-GREEN stretch tensor.

This RIVLIN equation can be reformulated as function of the trace 𝐼1 and residual invariants 𝐼′2 and 𝐼′3 with subtracted influence of the axiator by analogy with the axiatoric-deviatoric invariants of the stress or strain tensor [13,14]

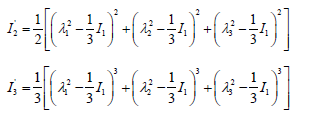
to exclude the superposition effects in the fitting of measured data.

The first order approximation provides the neo-HOOKE model W(𝐼1) = 𝑅100 (𝐼1 − 3). The truncated series of the second order

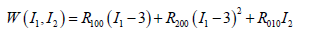
includes the MOONEY-RIVLIN model, cf. SATO [14, 15]. The third order approximation W(𝐼1, 𝐼2 ′ , 𝐼′ 3) for compressible materials

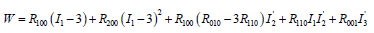
With this method, the impact of each term in the modified equation is easy to assess. For the FEM application, the parameters are converted back into the parameters of the original RIVLIN equation which allows the use of standard implemented routines.

Conclusion

Multiaxial test data are required for reliable material description. In addition to the uniaxial tensile test, the data from the planar tensile test and bulge test should be considered. In this paper, we discuss the valid test specification for the biaxial tensile test on soft biological tissues. The setup dimensions can be easily adapted to the properties of the specimen. The approximations are visualized in 𝜆 − 𝜎, the MOONEY plot, and further diagrams. Clearly better quality of the modelling is achieved. Our tests have gained acceptance in industry and research [15-17]. The scientists analyse the individual challenges of modelling elastomeric materials and provide expertise at all levels of the design process [18,19].

For more Articles on: https://biomedres01.blogspot.com/