Introduction
Cephalometry is one of the indispensable diagnostic tools in orthodontics for diagnosis of dentofacial problems, growth evaluation, treatment planning and outcome evaluation [1,2]. However, the most highlighted drawback still remains the representation of three-dimensional (3D) structures in twodimensional (2D) axis, leading to projection distortion, positional distortion, image magnification, landmark identification error, superimposition of structures which has partly frustrated clinicians particularly in the aspect of treatment evaluation [2- 4]. To overcome the drawbacks of 2D projection, Adams invented a correction formula for image enlargement and distortion [5]. Similarly, a compensator for lateral films was developed by Wylie and Elsasser which was later modified by Vogel to include PosteroAnterior (PA) cephalograms [6,7]. Savara also introduced a method to measure landmarks in three-dimension using lateral and PA cephalograms [8]. Additionally, in an attempt to combine the use of lateral and PA films together, Broadbent and Bolton introduced “Broadbent Orientator” which was an acetate overlay of lateral and PA film registered at Frankfort horizontal plane [1]. Additionally, Buamrind, et al.[9]. attempted to combine the use of two coplanar films based on the principle of photo-stereometry.
Cephalometry is one of the indispensable diagnostic tools in orthodontics for diagnosis of dentofacial problems, growth evaluation, treatment planning and outcome evaluation [1,2]. However, the most highlighted drawback still remains the representation of three-dimensional (3D) structures in twodimensional (2D) axis, leading to projection distortion, positional distortion, image magnification, landmark identification error, superimposition of structures which has partly frustrated clinicians particularly in the aspect of treatment evaluation [2- 4]. To overcome the drawbacks of 2D projection, Adams invented a correction formula for image enlargement and distortion [5]. Similarly, a compensator for lateral films was developed by Wylie and Elsasser which was later modified by Vogel to include PosteroAnterior (PA) cephalograms [6,7]. Savara also introduced a method to measure landmarks in three-dimension using lateral and PA cephalograms [8]. Additionally, in an attempt to combine the use of lateral and PA films together, Broadbent and Bolton introduced “Broadbent Orientator” which was an acetate overlay of lateral and PA film registered at Frankfort horizontal plane [1]. Additionally, Buamrind, et al.[9]. attempted to combine the use of two coplanar films based on the principle of photo-stereometry.
The study material comprised 22 dry dentate human skulls with mandibles. The samples were selected from a larger group based on inclusion criteria of having intact skull without any bony pathologic lesions, presence of permanent upper and lower incisors, presence of molars on both sides to maintain the vertical dimension, and having stable and reproducible occlusion.
Firstly, anatomical landmarks were examined and located on the mandible. The direct skull measurements of all samples were obtained manually using dental floss running along anatomical contour of mandible. The length of the dental floss was then confirmed by digital caliper (Absolute Digimatic Caliper, Mitutoyo, Japan). The measurements were as follows:
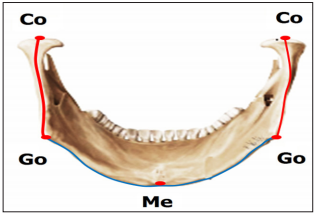
Ramal Height: Left and right ramal heights were measured from Condylion (Co) to Gonion (Go) on respective sides (Figure 1).
Mandibular Corpus Length: Left and right curvature of mandibular corpus lengths were measured from Gonion (Go) to the Menton (Me) as shown in Figure 1.
Figure 1: Direct skull measurement from mandible
a) Ramal height (R): Measured from Condylion (Co) to Gonion (Go).
b) Mandibular corpus length (MCL): Measured from Gonion (Go), to Menton (Me).
 Total Mandibular Length: The Left and right actual total mandibular length was the sum of ramal height plus mandibular corpus length. All the measurements were repeated twice and averaged for final comparison.
Total Mandibular Length: The Left and right actual total mandibular length was the sum of ramal height plus mandibular corpus length. All the measurements were repeated twice and averaged for final comparison.Tiny metallic balls were attached to all the identified landmarks: Condylion (Co), Gonion (Go) and Menton (Me)) using orthodontic wax. Subsequently, mandible was fixed with their respective skull according to the actual fossa to condyle relationship, with the dentition in maximum intercuspation. This position of the mandible was stabilized on several sites bilaterally and reinforced with a broad tape from the temporal bone of the skull to the mandible on both the sides. Each sample skull was then oriented in a cephalostat (Orthoceph® OC100 GE Healthcare, Finland) and stabilized with the help of bilateral ear rods in external auditory meatus. Frankfort horizontal plane was parallel to the floor for lateral and P-A cephalograms, while it was perpendicular to the floor for submento-vertex technique. Water level device was also used to check the skull position. Three 2D films in perpendicular directions to each other were taken for each skull, which include
a) Lateral (L),
b) Postero-anterior (PA) and
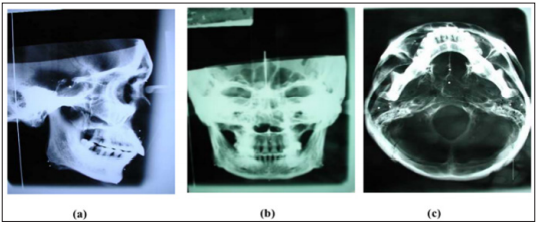
c) Submento-vertex cephalogram (SMV) (Figure 2).
Figure 2: Three different views of cephalometric films with attached metal balls.
a) Lateral cephalogram.
b) Postero-anterior cephalogram (PA).
c) Submento vertex cephalogram (SMV).
 Following radiation settings were followed throughout the process. The distance from mid-sagittal plane of skull to film was 9cm for lateral cephalograms, 15cm for PA cephalogram and 15cm for submento-vertex cephalogram respectively. The distance between the mid-sagittal plane of skull to radiation source was 5 feet. Radiation setting was adjusted at 69kVp, 15mA and exposure time of 0.64 seconds.
Following radiation settings were followed throughout the process. The distance from mid-sagittal plane of skull to film was 9cm for lateral cephalograms, 15cm for PA cephalogram and 15cm for submento-vertex cephalogram respectively. The distance between the mid-sagittal plane of skull to radiation source was 5 feet. Radiation setting was adjusted at 69kVp, 15mA and exposure time of 0.64 seconds.Following the tracing of the films, the XYZ coordinate axis system in this study was defined for each cephalogram as follows.
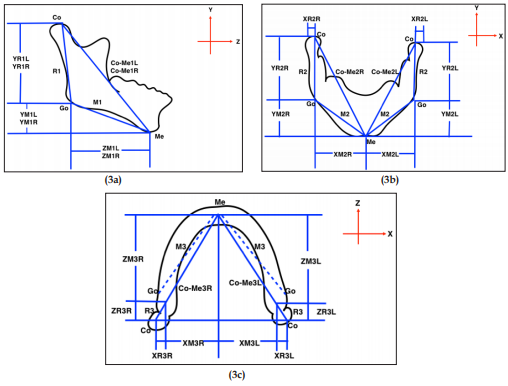
Lateral Cephalogram: ZY coordinate axis system with Frankfort horizontal plane as reference plane (Figure 3a).
Postero-Anterior (PA) Cephalogram: XY coordinate axis system with horizontal reference plane as a line connecting the medial aspects of the zygomatico-frontal sutures (Z) (Figure 3b).
Submento-vertex cephalogram: ZY coordinate axis system with sagittal reference plane as a line along vomer best fit (Figure 3c).
Figure 3: Geometry construction for three-dimensional coordinate axes (X, Y, Z) for formula derivation.
a) Lateral cephalogram. b) Postero-Anterior cephalogram (PA). c) Submento-Vertex cephalogram (SMV).
 Ramal height and mandibular body length were measured from all the three films of respective skull using digital caliper with the help of radiopaque metallic balls. The right and the left measurements were obtained separately. Measurements were also repeated twice and averaged for final comparison with the corresponding direct skull measurements of the same skull. Altogether, 40 variables (12 from lateral, 14 from PA and 14 from submento-vertex) were measured for ramal height and mandibular body length from set of three films for each skull. The operational definitions of the variables are mentioned in Tables 1-3 for lateral, PA and submento-vertex respectively. The radiographic measurements mainly comprised of:
Ramal height and mandibular body length were measured from all the three films of respective skull using digital caliper with the help of radiopaque metallic balls. The right and the left measurements were obtained separately. Measurements were also repeated twice and averaged for final comparison with the corresponding direct skull measurements of the same skull. Altogether, 40 variables (12 from lateral, 14 from PA and 14 from submento-vertex) were measured for ramal height and mandibular body length from set of three films for each skull. The operational definitions of the variables are mentioned in Tables 1-3 for lateral, PA and submento-vertex respectively. The radiographic measurements mainly comprised of:a) Anatomical landmarks distance and
b) Projected distance both along and perpendicular to the XYZ coordinate system.
Comparison was done for all the 2D variables to the corresponding direct skull measurement for both ramal height and mandibular corpus length categories.
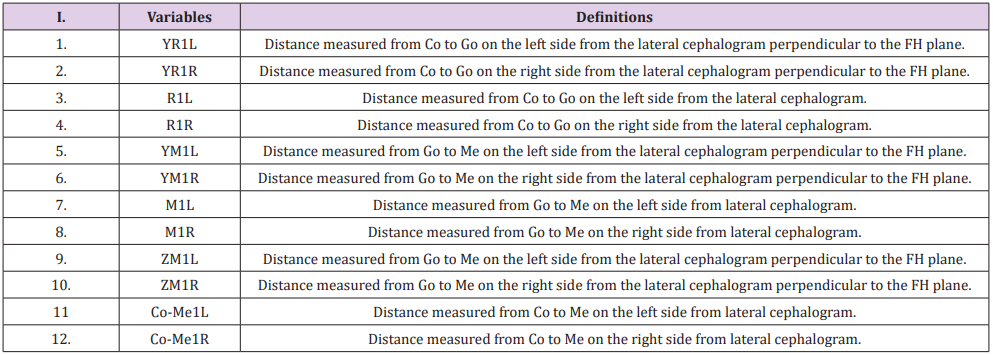 Table 2: Definitions of variables measured from Postero-Anterior (PA) cephalogram.
Table 2: Definitions of variables measured from Postero-Anterior (PA) cephalogram.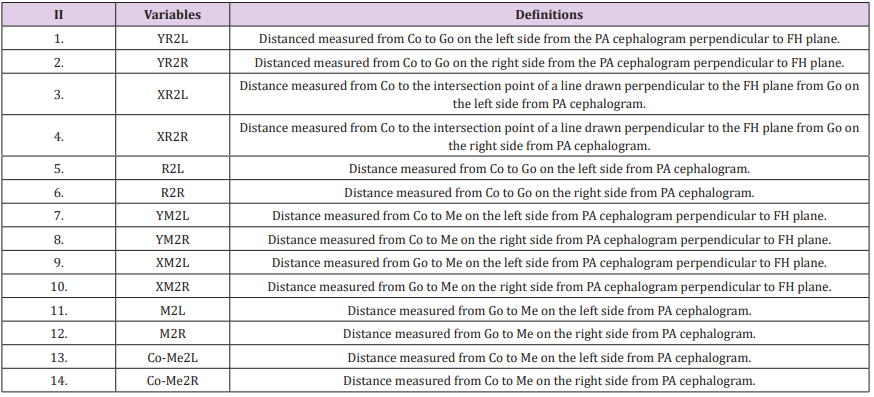 Table 3: Definitions of variables measured from Submento-vertex cephalogram.
Table 3: Definitions of variables measured from Submento-vertex cephalogram.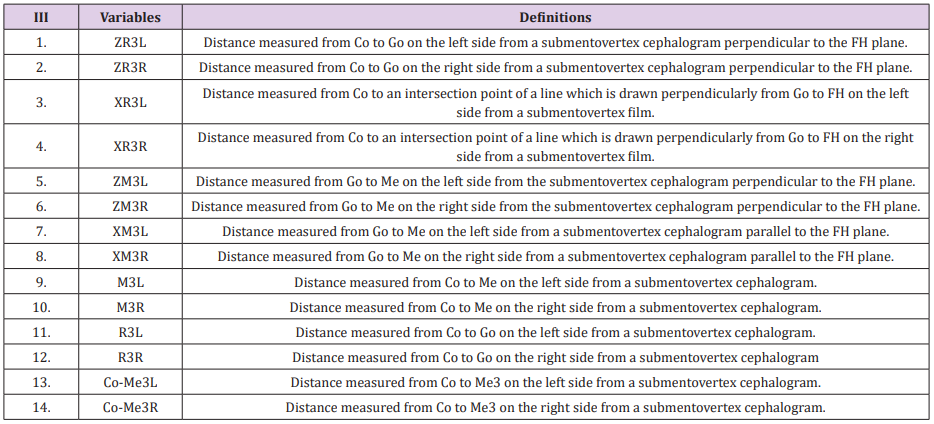 The differences were calculated by substracting the 2D measurements from the direct skull measurements. As depicted in Figure 3, the coding for each measurement starts with the coordinate axis, either X, Y or Z followed by R (ramal height) or M (mandibular body length). The numeric codes indicate 1(lateral), 2(PA) and 3(submento-vertex) cephalogram, whereas last alphabet R or L designate right or left side respectively. For example, YR1L means ramal height which was projected on Y axis, obtained from lateral cephalogram on the left side.
The differences were calculated by substracting the 2D measurements from the direct skull measurements. As depicted in Figure 3, the coding for each measurement starts with the coordinate axis, either X, Y or Z followed by R (ramal height) or M (mandibular body length). The numeric codes indicate 1(lateral), 2(PA) and 3(submento-vertex) cephalogram, whereas last alphabet R or L designate right or left side respectively. For example, YR1L means ramal height which was projected on Y axis, obtained from lateral cephalogram on the left side.The mathematical formula used in our study was developed based on algebraic Pythagorean theorem of right angle triangle [29]. The basic theorem equation for the two-dimensional rightangle triangle can be written as:
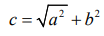
where “c” represent the hypotenuse and “a” and “b” are other two sides of the right-angle triangle respectively. For a threedimensional geometric figure illustrated in Figure 4a, to calculate the length of the side “s”, the value of “c” has to be calculated first. From the same figure, using Pythagorean theorem for 2-dimensional figures,
Figure 4:
a) 3-Dimensional geometric figure.
b) Three-dimensional coordinate axes (X, Y, Z) for formula derivation.
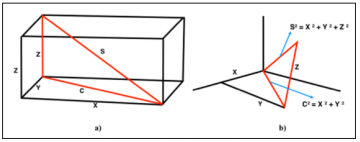 : c2 = x2 + y2 (1) and
: c2 = x2 + y2 (1) and: s2 = c2 + z2 (2)
Hence, combining equation (1) and (2)
: s2 = x2 + y2 + z2
Subsequently, using geometry construction applied to the measurements in three-dimensional coordinate axis (X, Y, Z) of the 2D cephalometric films as illustrated in Figure 3a-3c, different possible geometric formulas were derived. Basically, measurement variables across 2 to 3 cephalometric films were arbitrarily constructed. Hypothetically, 4 geometric formulas to calculate ramal height and 6 formulas to determine mandibular corpus length were derived as shown in Table 4. The formulas derived were then investigated for their validity by comparing with the direct skull measurements which represent the true measurement.
Table 4: Definitions of variables measured from Submento-vertex cephalogram.
 Data Analysis
Data AnalysisThe data analysis was performed with the SPSS (version 20.0, IBM Corp, Released 2011, Armonk, NY).
Normality Test and Scatter Plots: The data normality and distribution was tested with Shapiro-Wilk test which indicated normal distribution. Scatter plots were generated for 4 formulas of ramal height and 6 formulas of mandibular corpus length.
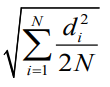
Results
Comparison Between Actual Skull VS. Cephalometric Measurements
Table 5 summarizes the mean of differences between the actual skull and 2D cephalometric measurements of ramal height (Co-Go) classified by type of cephalograms. All parameters revealed a statistically significant difference between actual skull measurements and 2D values obtained from 3 cephalometric films. In general, the values of projected (X, Y, Z) measurements showed greater mean of differences than direct measurements. The 4 measurements with least mean differences (values less than 1.5mm) in an ascending order were:
1) Ave R2 from PA cephalogram (1.22mm),
2) Ave. R1 from lateral cephalogram (1.27mm),
3) Ave. YR2 from PA cephalogram (1.30mm) and
4) Ave. YR1 from Lateral cephalogram (1.48mm). These values represent the closest value to the actual skull measurements.
Comparison Between Actual Skull VS. Cephalometric Measurements
Table 5 summarizes the mean of differences between the actual skull and 2D cephalometric measurements of ramal height (Co-Go) classified by type of cephalograms. All parameters revealed a statistically significant difference between actual skull measurements and 2D values obtained from 3 cephalometric films. In general, the values of projected (X, Y, Z) measurements showed greater mean of differences than direct measurements. The 4 measurements with least mean differences (values less than 1.5mm) in an ascending order were:
1) Ave R2 from PA cephalogram (1.22mm),
2) Ave. R1 from lateral cephalogram (1.27mm),
3) Ave. YR2 from PA cephalogram (1.30mm) and
4) Ave. YR1 from Lateral cephalogram (1.48mm). These values represent the closest value to the actual skull measurements.
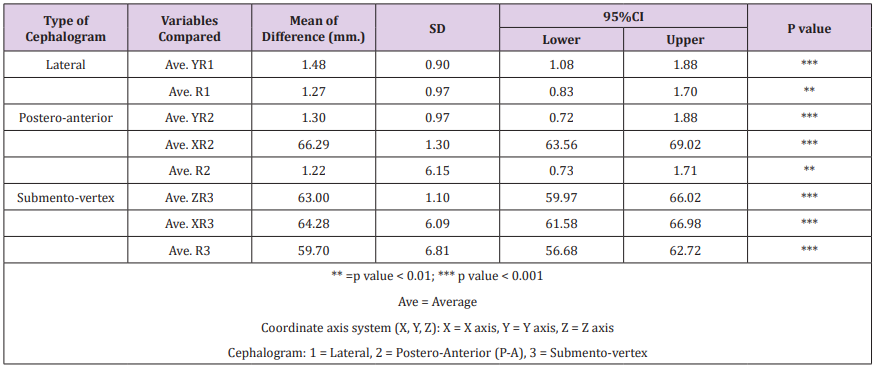 Table 6 summarizes the mean of differences between the actual skull and 2D cephalometric measurements of mandibular corpus length and total mandibular length. All parameters also showed a statistically significant difference between actual skull measurements and 2D values from 3 cephalometric films.
Table 6 summarizes the mean of differences between the actual skull and 2D cephalometric measurements of mandibular corpus length and total mandibular length. All parameters also showed a statistically significant difference between actual skull measurements and 2D values from 3 cephalometric films.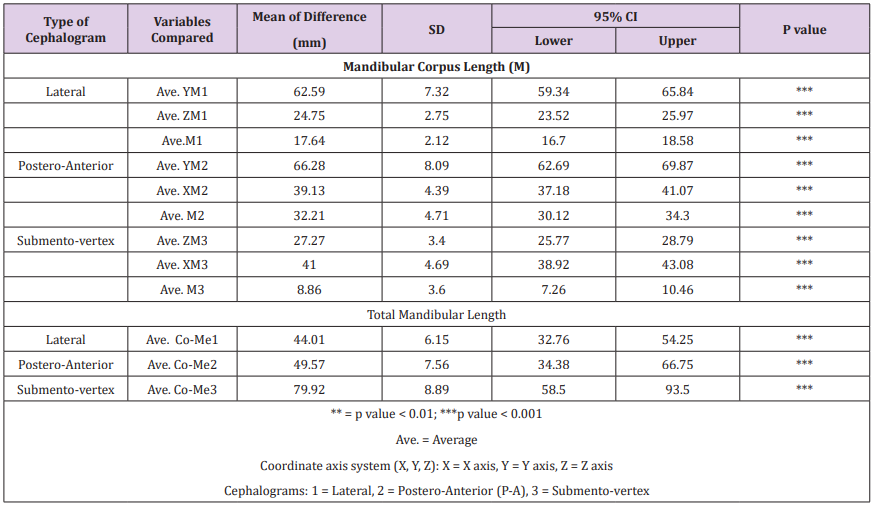 The lowest mean difference was recorded for submento-vertex film while all other variables had a vast difference with the actual skull measurements. The measurement with least mean difference was Ave. M3 from SV Cephalogram (8.86mm). Regarding total mandibular length, the least mean differences was recorded by Ave CO-Me1 from lateral cephalogram (44.01mm) followed by Ave COMe2 from PA cephalogram (49.57mm) and Ave. Co-Me3 from SV cephalogram (79.92mm) respectively
The lowest mean difference was recorded for submento-vertex film while all other variables had a vast difference with the actual skull measurements. The measurement with least mean difference was Ave. M3 from SV Cephalogram (8.86mm). Regarding total mandibular length, the least mean differences was recorded by Ave CO-Me1 from lateral cephalogram (44.01mm) followed by Ave COMe2 from PA cephalogram (49.57mm) and Ave. Co-Me3 from SV cephalogram (79.92mm) respectivelyTable 7 shows the mean of differences and Paired T-test comparison of measurements between 4 geometric formulas and actual ramal height. Three geometric formulas (R1, R2, R3) were successful in reducing the mean of differences to significant level, while R4 still shows between-group significance at p-value 0.03. R3 shows least mean of differences (0.41mm), followed by R1 (0.46mm) and R2 (0.65mm) respectively. Table 8 shows the mean of differences and paired T-test comparison of measurements between 6 geometric formulas and actual mandibular corpus length. All parameters demonstrated between-group significance except M4 which shows least mean of differences at 0.46mm.
 Table 8: Paired T-test comparison of measurements between direct skull versus 6 geometric formulas of mandibular corpus length (M).
Table 8: Paired T-test comparison of measurements between direct skull versus 6 geometric formulas of mandibular corpus length (M).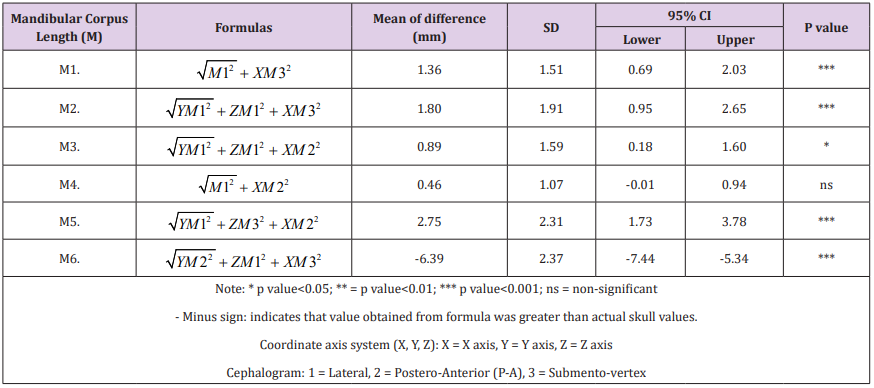 Scatter Plots of Data
Scatter Plots of DataAll scatter plots of 4 formulas of ramal height indicated excellent correlation of data with the best fit lines (r ranges from 0.91 – 0.95). Geometric formula 3 (R3) show the greatest r value of 0.953. All 6 scatter plots for mandibular corpus length indicated good to excellent correlation of data with the best fit lines (r ranges from 0.78 – 0.953). Geometric formula 5 (M5) showed the least r of 0.78 while Geometric formula 4 (M4) showed the greatest r value of 0.953.
Table 9 shows the results of Dahlberg’s error analysis calculated by repeating cephalometric measurements from 8 sample skulls. The errors for ramal height ranged from 0.31 (Ave.XR2) to 1.37 (Ave.YR1) whereas values of mandibular corpus length ranged from 0.56 (Ave. XM2) to 1.37 (Ave.YM1, Ave.M3).
 Power Calculation
Power CalculationUsing the value of M4 from Table 8, sample size of 22, Type I error rate, α = 5%, True mean, μ = 0.46mm., Null Hypothesis mean, μ0 = 1.5mm., standard deviation, σ = 1.0, the calculated power obtained for this study was 0.998 or 99.8% [30].
A new innovative approach of geometric formulas has been proposed which can accurately calculate ramal height and mandibular body length. We found significant disparity between skull measurement and 2D cephalometric measurements as reported in previous studies. The findings of this study supported the application of geometric formulas to calculate ramal height and mandibular body length more accurately whenever they are in question. For ramal height, the valid formulas were R1, R2, R3 as shown in Table 7, whereas for mandibular corpus length, the only valid formula was M4 as shown in Table 8. Accordingly, the validity of total mandibular length could be obtained from the combination of the valid values of ramal height and mandibular corpus length.
Orthodontists commonly used lateral films and seldom PA films to ascertain ramal height from Condylion to Gonion (Table 5). The findings in this study show that same measurement, AveR1 which represent the 2D Co-Go was slightly shorter than direct skull measures with a small mean difference of 1.27mm (95% CI: 0.83mm – 1.70mm) and 1.22mm (95% CI: 0.73mm – 1.71mm) for lateral and PA cephalograms respectively. This minute disparity was mainly assumed to be due to the divergence vector in rightleft (X axis) and antero-posterior direction (Z axis). Considering the fact that orthodontist mostly rely on lateral and PA cephalogram, this minor discrepancy could be slightly improved by using formula R2 in Table 8, which reduced the disparity to 0.65mm (95% CI: 0.03mm – 1.27mm). However, this minimal amount of reduction of around 0.6 mm may be considered clinically insignificant. Even though, R3 and R1 showed better results than R2, the fact that these 2 formulas resorted on using variables from submento-vertex film, may limit its practical use by the orthodontists.
Mean of difference of mandibular corpus length in Table 8 show that there exists a large disparity between direct skull and 2D cephalometric measurements. For mandibular corpus length, the 2D cephalometric measurements that orthodontist mostly follow was Go-Me from lateral cephalogram. We found that AveM1 which represent 2D measurement of Go-Me was markedly shorter than actual skull measures with the mean of 17.64mm (95% CI: 16.70mm – 18.58mm). This large disparity may be due to the failure of 2D radiographs to represent curvature of mandibular corpus, wideness in right-left (X axis), and the steepness of mandibular plane in vertical direction (Y axis). It is felt that these factors contributed for a large difference in the mean between the 2D cephalometric measurements and direct skull measurements.
Co - Me still is a popular parameter used by orthodontist to represent total mandibular length. When we compared the Ave CoMe from 2D cephalometric films with the actual total mandibular size (the sum of ramal height plus mandibular corpus length of actual skull), we noticed a huge difference between the two values. Ave Co-Me1 from lateral cephalogram was on average 44.01mm shorter than actual skull measurements. This disparity became even worst in Ave Co-Me2 from P-A cephalogram. Due to this observation, we proposed that cephalometric Co-Me measurement was not appropriate to represent the total mandibular length as orthodontists assumed in the past. Hence, using cephalometric CoMe would underestimate the total mandibular size to a great extent which may lead to misinterpretation of the treatment results.
The available literature supported the existence of significant difference between the direct skull measurements and 2D cephalometric measurements [34-37]. Whether cephalometric or direct skull measurements is greater may depend on the type of films with inherent magnification, projection error and skull anatomy characteristics. The finding of the current study concurs with the study of Farkas LG et al. [34] where they reported that both singular and paired measurements from PA cephalograms were significantly shorter than direct skull measurements. This mismatch between direct skull and cephalometric measurements was attributed to the nature of two-dimensional films exhibiting distorted image of three-dimensional objects.
Durão et al. [38] in 2014 observed that seven of the total ten linear measurements evaluated were greater on 2D radiographs while compared to gold standard skull measurement. However, three measurements involving Co-Gn, Co-ANS, Go-Gn were larger when measured directly on skull. Go-Gn and Co-Gn which corresponds to Go-Me and Ave CoMe in our study, was observed to be greater when measured directly on skull. Our finding was generally in agreement with their observation. We found that 2D measurements of ramal height, mandibular corpus length and total mandibular length was shorter than actual skull (Tables 5 & 6). It was however, interesting to observe that the mean difference of GoMe in our study was much larger (17.64mm) while Durão et al. [38] reported the difference of only 0.45mm. This was probably due to different methodologies employed in the two studies. In our study, Go-Me was measured following the curvature of mandibular body, whereas they used a mere linear distance between Go to Me. It can therefore be stated that radiographic linear measurements can significantly underestimate the actual measurement of the skull. Therefore, clinicians must be extra cautious while reporting the results. Additionally, our findings also substantiate the statement put forward by Moyers and Bookstein [39] that cephalometric measurements are inefficient and fail to capture the measurements of the curved structures.
In actual patient, measurement could be subjected to more error since metallic markers cannot be placed. Thus, it may be more difficult to control factors that contribute to error. Moreover, application of some formulas containing variables from submentovertex film may be impossible due to the ambiguity of landmarks like condylion and gonion without radio-opaque metal markers. Lateral cephalograms may present differential enlargement between the left and right side. Thus, it may be more difficult to control several factors that contribute to error in live patient.
Although, 3D CBCT have become increasingly popular, cephalometric radiographs are still widely used by practitioners around the world due to the virtues of being economical and less radiation exposure. Moreover, 2D cephalometrics have normative database and are more practical for quantitative or long-term serial analysis. The findings of this study confirmed that there exists a significant disparity between direct skull measurement and 2D cephalometric measurements. This suggested that clinicians must be cautious while interpreting dimension changes of mandible from 2D cephalograms. Our results found that geometric formulas can be applied to calculate ramal height and mandibular body length more accurately. This current approach may prove to be an effective alternative to evaluate the effects of functional appliance on ramus and mandibular body by comparing pretreatment and posttreatment measurements. Future studies may focus on comparing the geometric formulas with the 3D CBCT techniques and also apply the geometric formulas to evaluate the effects of orthopedic appliances on ramus and mandibular body.
a) All 2D cephalometric mandibular measurements were significantly shorter than direct skull measurements.
b) Average ramal height and mandibular corpus lengths measured from Lateral cephalometry was 1.27 mm. (SD 0.97) and 17.64 mm. (SD 2.12) shorter than from actual skull respectively
c) Geometric formulas significantly reduced mean difference between values from 2D cephalometrics and skull thereby the ramal height and mandibular corpus length were more accurate.
d) Valid formulas for ramal height were
i.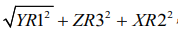 followed by
followed by
ii.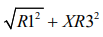 and
and
iii.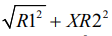 , whereas the only valid formula for mandibular corpus length was
, whereas the only valid formula for mandibular corpus length was 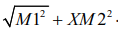 .
.
i.
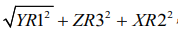 followed by
followed byii.
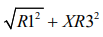 and
andiii.
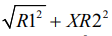 , whereas the only valid formula for mandibular corpus length was
, whereas the only valid formula for mandibular corpus length was 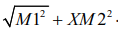 .
.Developing a Functional Staging to Assist Clinical Interpretation of the Oswestry Disability Indexs-https://biomedres01.blogspot.com/2020/10/developing-functional-staging-to-assist_20.html
More BJSTR Articles : https://biomedres01.blogspot.com

No comments:
Post a Comment
Note: Only a member of this blog may post a comment.