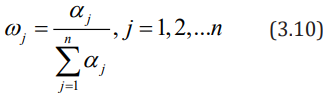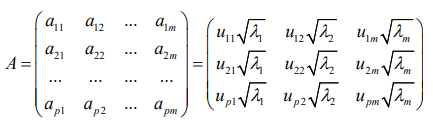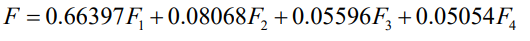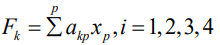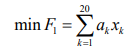Biomathematical Model Study on the Opioid Crisis in
America
We discuss the extent of opioids flooding, and establishes a
dynamic panel data model for characterization and prediction
of crisis, using generalized moment estimation and time series
analysis to solve the model; the grey relational analysis is carried
out to judge whether the use of opioids is related to population
data, and the principal component evaluation model is established
to verify the results; the linear programming model was analyzed
using the sensitivity analysis for the validity of the test strategy.
First, a multi-dimensional descriptive statistical analysis of the
data, and found the geographical distribution of opioids. The data
was organized into panel data. On the one hand, the dynamic panel
data model was established, and the parameters were estimated
by generalized moments. It was concluded that the heroin should first appeared in 1910, OH-HAMILTON and synthetic opioids first
appeared in 1939 PA-PHILADELPHIA. On the other hand, the
Hierarchical Cluster based on the panel data of “absolute quantity”,
“fluctuation”, “skewness”, “kurtosis” and “trend” feature extraction
is used to find out the five counties that need the most concern in
the US.
And time Series Analysis was used to find the year when these
counties reached the drug threshold, and the threshold level was
obtained by the dynamic panel data model. For example, the threshold for
the number of synthetic opioid cases in OH-CUYAHOGA in
2018 was 6783. To judge whether the use of opioids is related to
US population data, use gray correlation analysis to find the ratio
of the number of heroin and synthetic opioid cases in the county to
the total number of identified substances. The correlation between
the two and the selected first-level indicators from the population
data is greater than 0.5, indicating that the degree of association
between them is greater. To verify the five counties that may cause
the US to panic, the entropy weight method is used to select 16
indicators, and the indicators in the NFLIS are combined to establish
a comprehensive evaluation system for the degree of opioid flooding and
principal component evaluation model. The comprehensive
weighted scores were used as the class of opioid flooding scores,
and the 461 counties in 8 years were distributed according to the
frequency distribution of F values, and the degree of opioid abuse
was divided into three levels: severe, general and lower.
We propose the strategies for combating the opioid crisis: the
US can stipulate that all people must have completed the 12th grade
compulsory education when they are 25 years old. To test the
effectiveness of the strategy and determine the range of important
parameters, a sensitivity analysis of linear programming was used.
Taking min F1 as the objective function, a constraint condition is
formed between the 20 indicators, and the parameter range (c,k)
of each index is obtained by local sensitivity analysis. The obtained
parameter range is brought into the first principal component
expression, and it is determined whether the parameter range is valid
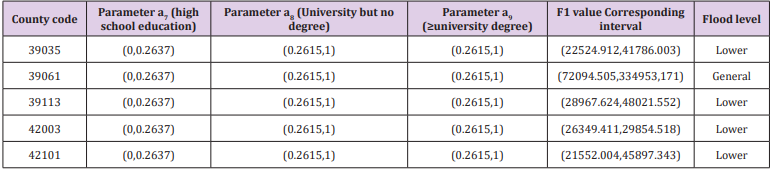
according to the level of the F1. In the end, the parameters of high
school education, university but no degree and university degree
and above are correct (0,0.2637), (0.2615,1), (0.2615,1), and the
flood levels of the four counties are correct. Has been reduced to a
lower level, only Hamilton County, Ohio’s hazard level reduced to a
general conclusion, which shows that the strategy is effective.
Biomathematical Modelling
Multidimensional Descriptive Statistical Analysis Model:
This study investigates the data concerned with opioid crisis from
461 counties in the five states from 2010 to 2017, with a total of
24,063 samples and 61 substance name.
a) Counties: The data can be sorted out. In the 461 counties,
not every county has an incident report every year. The reason may
be that the data of the current year is difficult to obtain, or the data
of the year is 0, so it is omitted. However, we believe that either case
can indicate that the county’s drug abuse has not reached a serious
level. Combined with the data of each county, the counties with
missing data have fewer drugs in the few years with data, close to
zero, so we fill the value of the drug that was missing in the county
from zero.
b) Substance Name: The name of the substance identified
in the analysis contains 47 synthetic opioids and 13 non-synthetic
opioids, these 13 non-synthetic drugs are Codeine, Dihydrocodeine,
Acetylcodeine, Acetyldihydrocodeine, Morphine, Heroin, Hydromorphone,
Oxycodone, Oxymorphone, Buprenorphine, Hydrocodone, Nalbuphine,
Dihydromorphone.
c) YYYY & FIPS_ Combined: The time and county code data
are all integers, and the distance between the data is the same, so the
two columns of data are logarithmically transformed to make the
data better visualized, and the difference between the two columns
is small, especially year. Therefore, the logarithmic transformation
is performed with a base of 1.1.
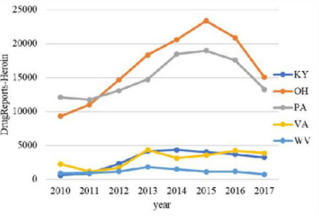
The overall trend of the number of drugs in the five states from
2010 to 2017 and the overall trend of the number of heroin were
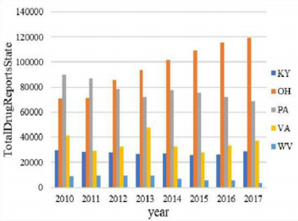
analyzed. The resulting bar chart is shown in Figures 1 & 2. It can
be seen intuitively from Figure 1 that the total number of drugs in
KY and OH states is far greater than the other three states. Among them,
the OH state has increased year by year, the PA state has
decreased year by year, the VA state has fluctuated greatly, and the
KY state and the WV state have stabilized at a lower value. As can
be seen from Figure 2, the number of heroin in these five regions
increased first and then decreased over time. The turning point is
probably in 2015, and the number of heroin in OH and PA states is
much higher than in the other three states. Therefore, PA State and
OH State are the targets of key observations.
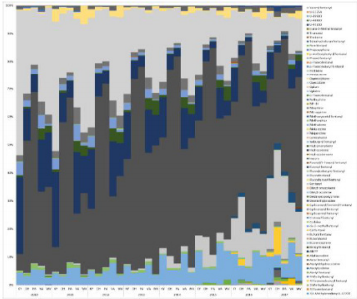
Further analysis of the change in the proportion of the substance
identified in the analysis from 2010 to 2017, the resulting percentage
of the accumulated area is shown in Figure 3. The greater the
proportion of color in the percentage stacked graph, the greater the
proportion of the substance in the analysis. It can be seen from Figure 3
that heroin (dark brown part of Figure 3) accounts for the
most, nearly half. Followed by Oxycodone (light grey), the proportion of
other substances is much smaller than heroin. Continue to
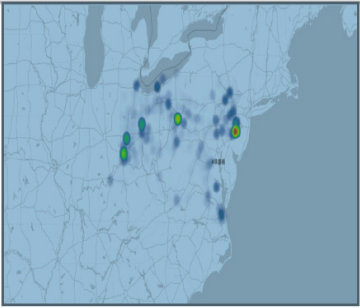
observe the geographical distribution of the number of heroin, as
shown in Figure 4. It can be seen from Fig. 4 that heroin is
concentrated in five counties, and the codes according to the
distribution
order (FIPS) are 39035, 39061, 39113, 42003, 42101.
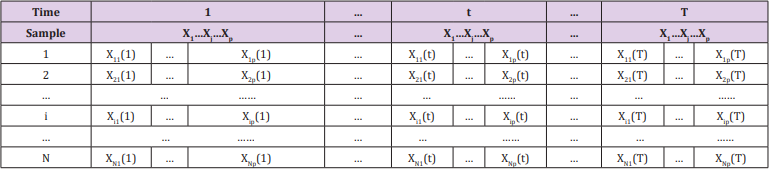
The Establishment of Dynamic Panel Data Model: The data
given in the title is multi-indicator panel data. In order to facilitate
the observation of indicators, the data is organized into the form of
Table 1. Strictly speaking, it should be represented by a
three-dimensional table. For ease of understanding and explanation, the
following two tables are still used. As shown in Table 1, there are a
total of N samples in the study. Each sample has T records and p
indicators per period. Then the value of the j-th indicator of the
sample i
in the t-th period is X t ij ( ), where i Nj pt T = = = 1, 2... 1, 2...
1, 2... ,
the difference between this table and the simple two-dimensional
table is that it contains three-dimensional information such as time,
sample and indicator.
Data Pre-processing: The data of time and county code are integers, and the distance between the data is the same, so the two
columns of data are logarithmically transformed to make the data
better visual, and the difference between the two columns is small,
especially time. Therefore, the logarithmic transformation is performed with a base of 1.1.
Dynamic Panel Data Model Establishment: Since the title requires determining the earliest position used by the specific opioid,
the quantization model is prioritized to incorporate the position as
a variable into the model to solve the earliest position. Therefore,
the regression model is used. The initial model is as follows
Among them, Y represents the number of drugs identified in
each county, X1
represents the code of each county, X2
represents
time (yearly), and X3
represents the ratio of the number of identified
drugs in each county to the total number of confirmed drug cases
in the county for we believe that the ratio can reflect the degree of
development of drugs to some extent.
Considering the inducibility and infectivity of drugs, the drugs
that lag behind the first phase should have an impact on the previous
period. Therefore, the lag phase is included as an explanatory
variable in the model, and the first-order lag variable is considered.
Since the explanatory variables contain both time variables and
regional variables, and cover both time series data and crosssection
data, the dynamic panel data model is finally adopted. Since
the number and proportion of drugs have zero values, the initial
model (3.1) is adjusted as follows.
where Yit the number of drugs identified in the t-th year of the
i-th county
Model Solving and Analysis: In the dynamic panel data model,
due to the existence of the lag-interpreted variable, it is possible
that the explanatory variable is related to the random error term,
so that the estimators obtained by using OLS and GLS are biased
and non-uniform. Ahn and Schmidt (1995) and Judson and Oewn
(1999) used Generalized Moments (GMM) to study the parameter
estimation of the dynamic panel data model, the statistical
properties of the estimates and the model checking methods [3].
The core idea of GMM estimation is to use tool variables to generate
corresponding moment conditions.
According to the estimation idea of GMM, the model (3.2)
is estimated by EVIEWS software, and the hysteresis order is
determined according to whether the t-test of the parameter
estimation has robustness. The result is as follows.
a) Section 1: Heroin
It can be seen from the above formula that the adjusted R
square is 0.849, and the fitting effect is general, and X1
does not pass
the 10% t test. However, the correlation matrix shows that there is
no multicollinearity between X1
and other explanatory variables, so
the data is adjusted to raw data. The model is improved as follows.
Among them, the t-statistic is in the brackets, *** indicates that
it is significant at the level of 0.05, and * indicates that it is significant
at the level of 0.1. Except for the dynamic panel data model, the
county code is significant at the level of 0.1, and other estimates
are significant at the 0.05 level, indicating that the regression effect
is good.
b) Section 2: Synthetic Opioid
It can be seen from the above formula that the adjusted R square
is 0.949, and the fitting effect is good, and each explanatory variable
has passed the significant level of 0.01. The earliest appearance of
opioids must have never appeared before and began to grow after
emergence. Therefore, the panel data model can be used to make
Yit=0, then Yi(t-1) and ratio are 0. To find the earliest position, we hope
that the year is as small as possible. We have obtained a quantitative
relationship between the area and the number of drugs, so that the
year can be reduced in turn, and the corresponding county codes
are obtained separately. In the case of Heroin, when the year is
reduced to 1910, the corresponding county code is 39061. When
the year is reduced to 1909, the county code has been reduced to
four digits, which is inconsistent with the data.
Therefore, 1910 is considered to be Heroin. Because of the
earliest year, the earliest position corresponding to the occurrence
is 39061 (OH-HAMILTON). The earliest appearance time of
synthetic opioids is 1939, and the earliest position is 42101 (PAPHILADELPHIA).
Time Series Model Based on System Clustering
Five Feature Extraction of Panel Data: Several statistics for
the multidimensional indicator panel are given below, and the
statistic feature extraction will use these statistics. The mean and
standard deviation of the j th indicator T period of sample i are:
a) Standardization of Panel Data
Due to the difference in the dimension and magnitude of
the indicator, it will have an impact on the final analysis results.
Therefore, the standardization process of the mean of Xij (t) is
first performed, and the standardized data is set to Xij
*
(t), and the
standardized formula is due to the difference in the dimension
and magnitude of the indicator, it will have an impact on the final
analysis results. Therefore, the standardization process for the
mean value is first set, and the standardized data is
among them, 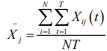 ,after standardization, the mean
value of each indicator is 1, and the variance is
,after standardization, the mean
value of each indicator is 1, and the variance is
The variance of each index after such standardization is the
square of the coefficient of variation of each index, which not only
eliminates the influence of dimension and magnitude, but also
retains the variation information of the original indicator.
b) Feature Quantity Extraction of Panel Data Indicators
According to the extraction of the feature quantity of panel
data in the literature [4], this paper defines the feature quantity
sof each index during the inspection period from the aspects of
development level, trend, fluctuation degree and distribution of the
indicator period. For the panel dataset 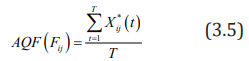 , there are N samples,
each sample records T, and there are p indicators in each period.
, there are N samples,
each sample records T, and there are p indicators in each period.
i. Definition 1: The jth indicator of the sample i is the fulltime Absolute Quantity Feature, abbreviated as AQF(Fij)
AQF (Fij)is actually the mean of the jth indicator of sample
i over the total period T, which reflects the absolute level of
development of the jth indicator of sample i in the analysis time
domain (over the entire period).
ii. Definition 2: The jth indicator of the sample i is the fulltime “Variance Feature”, abbreviated as VF(Fij)then
Among them, 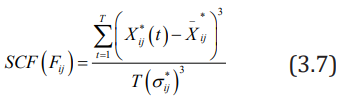 in definition 1, which
reflects the degree of fluctuation of the jth index of sample i over
time.
in definition 1, which
reflects the degree of fluctuation of the jth index of sample i over
time.
iii. Definition 3: The jth indicator of the sample i is the fulltime Skewness Coefficient Feature, abbreviated as
Where, 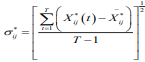 represents the standard deviation of the
jth index of the sample i over the entire period, SCF (Fij) reflects the
degree of symmetry of the jth index of the sample i over the entire
period, SCF F( ij)˂ 0, indicating that most of the index is located to
the right of the average, SCF (Fij)˂ 0, indicating that most of the
indicators are located to the left of the average.
represents the standard deviation of the
jth index of the sample i over the entire period, SCF (Fij) reflects the
degree of symmetry of the jth index of the sample i over the entire
period, SCF F( ij)˂ 0, indicating that most of the index is located to
the right of the average, SCF (Fij)˂ 0, indicating that most of the
indicators are located to the left of the average.
iv. Definition 4: The jth indicator of the sample i is the
Kurtosis Coefficient Feature, abbreviated as KCF(Fij).
KCF (Fij) reflects the sharpness of the distribution curve of the
jth indicator of sample i over the entire period. KCF (Fij) ˃ 0 indicates
that the distribution of the index value is more dispersed than the
normal distribution, and KCF (Fij) ˂0 indicates that the distribution
of the index value is more concentrated around the average value
than the normal distribution.
v. Definition 5: The jth indicator full-time “Trend Feature”
of sample i, abbreviated as TF(Fij), the long-term trend of the TF(Fij)
indicator. If the TF(Fij) value of the indicator is closer, it means that
both indicators show the same slope change and the closer the two
indicators are.
Indicator Selection
According to the previous analysis of the data and the variables
of the demand, feature extraction of the following indicators:
Heroin, non-synthetic opioids, Synthetic opioid, opioids, Total Drug
Reports County
Extraction Results
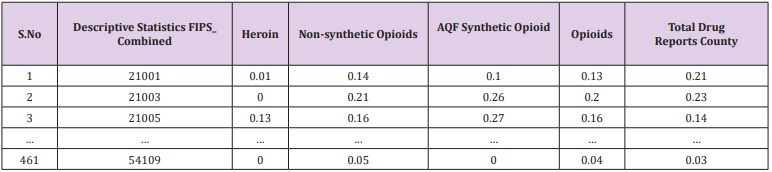
Take the Absolute Quantity Feature as an example. The final
data obtained is shown in Table 2 below. In order to visually
see the data characteristics of different indicators in the time
dimension between the county and the county, take the Absolute
Quantity Feature as an example and make an observation chart of
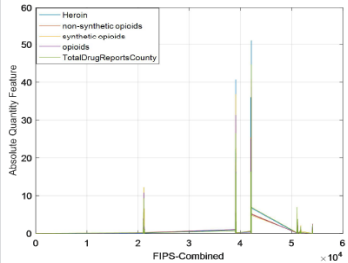
five indicators. The obtained line chart is shown in Figure 5. The
abscissa in Figure 5 indicates (total coding) FIPS_ Combined, the
ordinate indicates the AQF value corresponding to each county,
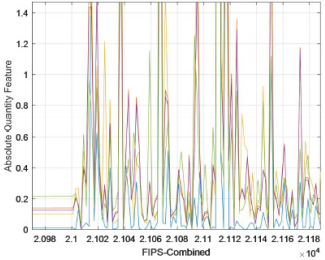
and Figure 6 is a partial enlarged view of Figure 5. As can be seen
from Figures 5 & 6, the fluctuations of these indicators are similar.
Explain heroin, non-synthetic drugs, synthetic drugs, opioids, total
drug counts in Total Drug Reports County. These indicators have
similar development levels throughout the period from 2010 to
2017, and each county has its own characteristics.
Cluster Data Clustering Results
The five characteristics extracted from the panel data index
were systematically clustered with heroin and synthetic opioids.
The obtained pedigree map is shown in Appendix’s 1-4. The
systematic clustering results of synthetic opioids and the systematic
clustering results of heroin. Consistent, see Appendix 2 for details.
The clustering results are shown in Table 3. The results of the two
system clusters pointed out that the five counties, CUYAHOGA,
HAMILTON, MONTGOMERY, ALLEGHENY, and PHILADELPHIA, are
the two counties with the largest number of heroin cases and the
most counties with the largest number of synthetic opioid cases.
Counties are the top priority areas in the United States that require
major concerns.
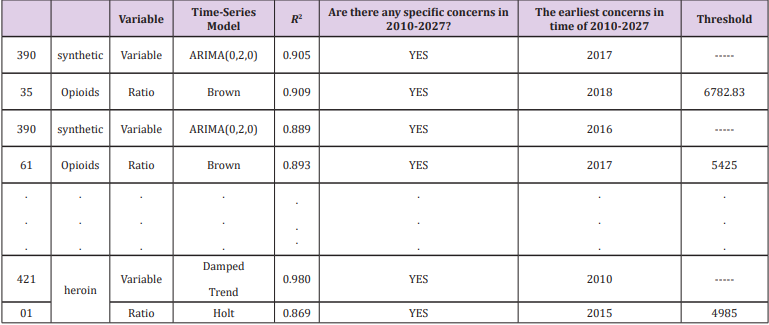
Time-Series Model: The panel data includes time series data
and cross-section data. We have obtained five key counties (39061,
39035, 42101, 39113, 42003) in the previous section. Now we
analyse the time and space characteristics of the data in these
five counties. Based on the extracted features for clustering, the
clustering results have depicted the absolute number of specific
drugs from this perspective. To extract more relevant information
from the data provided by NFLIS, we use the county’s specific drugs
and the county’s total The ratio of the number of drugs is derived
data, and time series analysis is performed. The final results of the
2010-2017 consecutive year time series analysis of the heroine
ratio and the synthetic opioid ratio of the five counties in the five
counties are shown in the following Table 4.
Reference [5] mentions the statistical analysis of data from
previous years, The number of cases of abusive use of opioids in
a state accounted for about 20% of the number of cases of drug
deaths in the state, which already reflects the seriousness of the
abuse of opioids. We borrowed this ratio to indicate that when a
county’s abuse of opioids accounted for 20% of the number of drug
use cases in the county, it indicated that the situation was critical
and relevant government departments should pay great attention
to this. Therefore, the arguments such as the position of the
sequence indicating the “ratio” and the year when the ratio reaches
20% are brought into the dynamic panel data model, and the critical
value of the independent variable Yit , that is, the threshold of the
corresponding sequence can be obtained separately
Principal Component Evaluation Model Based on
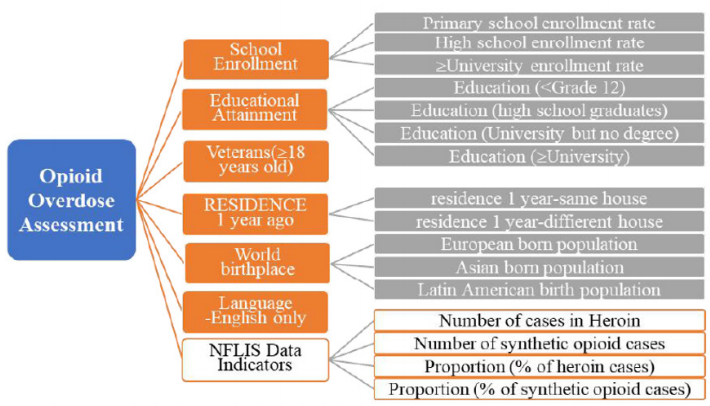
Entropy Weight Method
Data Analysis and Processing: We need to analyze the
common variables of the counties shared by the seven-year data,
and by comparison, we find that each observation has four forms
(Estimate; Margin of Error; Percent; Percent Margin of Error),
and what we need is the estimated amount, and the variables and
counties in the annex from 2010 to 2016 are not exactly the same.
The data of the four tables from 2010 to 2013 are the same as the
individuals, and the variables of the three tables are the same as
the individuals from 2014 to 2016. For example, from 2010 to 2013
(county code) GEO.id2 has 51515, and the county code from 2014
to 2016 does not have this county. From 2010 to 2013, there are
no variables (COMPUTERS AND INTERNET USE - Total Households,
COMPUTERS AND INTERNET USE - Total Households - With a
computer, COMPUTERS AND INTERNET USE - Total Households -
With a broadband Internet subscription).
Therefore, the relevant individuals of 51159, 51161, 51685 in
the variable GEO.id2 are deleted. In the same way, the variables
common to the seven years are screened for analysis. After the
above treatment, 149 variables and 464 samples (counties) were
obtained. And we need to analyse the data of the first question. And
similarly, screen out the same county in the first two questions,
and finally get 460 samples. After excluding the variables with
unreasonable estimates and error ranges, we will select the
variables we need from the remaining variables according to the
literature and topic requirements, and finally get 21 variables to
classify the data such as educational achievements. Variables of
less than nine years and education levels of nine to twelve years
are aggregated, new indicators are obtained for education levels
below 12 years, and so on, and the four key points included in
the first question are included. From the variable to the second
question indicator, the last 22 variables selected initially are shown
in Appendix 6.
Grey Correlation Analysis: There are known information in
the objective world, as well as many unknown and unconfirmed
information. Known information is white, unknown or nonconfirmed information is black, and between the two is gray. The
grey concept is the integration of the concepts of “less data” and
“information uncertainty”. The grey system theory is aimed at
this kind of uncertainty problem with neither experience nor
information, that is, the problem of “less data uncertainty”. The grey
system theory regards the uncertainty as the amount of gray. In
essence, it is a mathematical theory to solve the uncertainty theory
of information deficiency.
Because the gray system has less data and incomplete
information, it is difficult for decision makers to determine
the quantitative relationship between factors. It is difficult
to distinguish the main factors and secondary factors of the
system, thus introducing the gray correlation analysis method.
A comprehensive evaluation method based on the grey system
theory--grey correlation analysis method is to measure the
degree of correlation between factors according to the similarity
or dissimilarity between the developmental trends of factors
and quantifies or orchestrate the factors between systems with
incomplete information. According to the theory of grey relational
space, the original data needs to satisfy the dimensionless or the
same dimension. In this paper, the extremum method is used to
dimensionize the original data, and the processed data is combined
with the ideal object data column to obtain a new matrix:
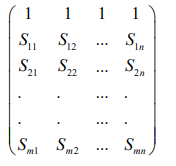
Record Si = (Si1,Si2,....,Sin),i=0,1,....,m,S0 as the reference
sequence, and calculate the correlation coefficient layer βi ( j) of
the jth index of Si
and the jth index of S0(i = 1, 2,....,m; j = 1, 2,...,n ) ,
In the above formula ρ ϵ [0,1], generally takes ρ=0.5
By calculating as above, the correlation coefficient matrix β is
obtained:
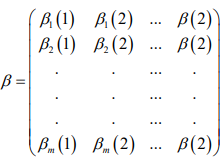
Let 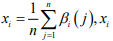 is the degree of association between the i-th
evaluated object and the ideal object. The merits of the object to
be evaluated are evaluated according to the size of the xi
value.
The larger the xi
, the higher the degree of association between the i-th evaluated object
and the ideal object, and thus the better it is
among all the evaluated objects. Because the topic requires judging
whether the use or use trend of opioids is related to the socioeconomic
data of the census, and the part 2 data shows the rules of
the first-level indicators and the second-level indicators, of which
there are 7 first-level indicators. Combining the use and use trends
of opioids (represented by the number of drug cases in each county
and the number of drug cases in each county and the total number
of identified drug cases), the gray correlation analysis is carried out
on 9 indicators. The correlation degree is solved by using MATLAB.
The specific procedure is shown in Appendix 3. As can be seen
from the above results, all correlations are greater than 0.5. As can
also be seen from Appendix 2, the correlation coefficient matrix
is close to 1, indicating that the use or use trend of opioids has a
strong correlation with all aspects of the population.
is the degree of association between the i-th
evaluated object and the ideal object. The merits of the object to
be evaluated are evaluated according to the size of the xi
value.
The larger the xi
, the higher the degree of association between the i-th evaluated object
and the ideal object, and thus the better it is
among all the evaluated objects. Because the topic requires judging
whether the use or use trend of opioids is related to the socioeconomic
data of the census, and the part 2 data shows the rules of
the first-level indicators and the second-level indicators, of which
there are 7 first-level indicators. Combining the use and use trends
of opioids (represented by the number of drug cases in each county
and the number of drug cases in each county and the total number
of identified drug cases), the gray correlation analysis is carried out
on 9 indicators. The correlation degree is solved by using MATLAB.
The specific procedure is shown in Appendix 3. As can be seen
from the above results, all correlations are greater than 0.5. As can
also be seen from Appendix 2, the correlation coefficient matrix
is close to 1, indicating that the use or use trend of opioids has a
strong correlation with all aspects of the population.
Principal Component Evaluation Model Based on Entropy
Weight Method: According to the idea of information entropy,
entropy is an ideal scale when evaluating the index weight of
indicator system. The principal component analysis method has
a good dimensionality reduction processing technology, which
can transform multiple indicators into several uncorrelated
comprehensive factors, and the comprehensive factor variables
can reflect most of the information of the original index variables,
which can better solve many problems. Requirements for
indicator evaluation. Therefore, a principal component evaluation
model based on entropy weight method can be established.
Consider an indicator evaluation system, in which there are n
evaluation indicators, m evaluated objects, and the raw data of the
corresponding indicators of the evaluated objects are represented
by the following matrix form.
First, the raw data is dimensionless:
Remember that the optimal value for each column in R
(Note: The profitability indicator is that the larger the index
value, the better. The cost index is the smaller the indicator value,
the better.)
After the original data is dimensionless, it is recorded as a
matrix S = (Sij)mxn
Normalize S, remember
The 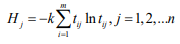 obtained in this way does not destroy the
proportional relationship between the data.
obtained in this way does not destroy the
proportional relationship between the data.
Define the entropy of the jth evaluation indicator as
Where 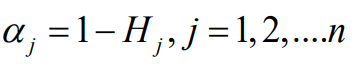 (so the chosen k is such that,
0≤Hj≤1, convenient for subsequent processing)
(so the chosen k is such that,
0≤Hj≤1, convenient for subsequent processing)
Define the difference coefficient of the jth evaluation indicator
as
Define the entropy weight of the jth evaluation indicator as
The entropy weight thus defined has the following properties:
a) When the values of the evaluated objects on the index J are
exactly the same, the entropy value reaches the maximum
value of 1, and the entropy weight is zero, which means that
the indicator does not provide any useful information to the
decision maker, and the indicator can be considered to be
cancelled.
b) When the values of the evaluated objects on the index
J differ greatly, the entropy value is small and the entropy
weight is large, which means that the indicator provides useful
information to the decision maker, and in the problem, each
object is in the There are obvious differences in indicators,
which should be focused on;
c) The larger the entropy of the indicator, the smaller its entropy
weight, and the less important the indicator is. The entropy
defined by equation (3.10) satisfies:
It can be seen from the above discussion that the entropy
weight method reflects the importance of the difference between
the observations of the same indicator. The final indicators are as
shown in Figure 7 below.
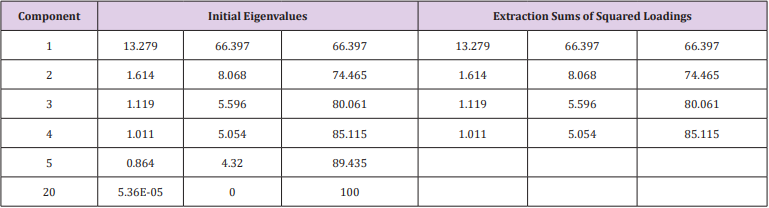
Solution and Result: The above 18 indicators can be obtained
by SPSS factor analysis to obtain the factor load matrix and the
variance interpretation ratio (Table 5). The variance interpretation
scale table is as Table 6, the first four components are extracted, and
the factor load matrix is shown in Appendix 5. It can be seen from
Table 6 that the first four principal components explain 85.115% of
the overall properties, that is, 85% of the features can be explained
according to the first four principal components. Therefore, the
first four principal components are analyzed here.
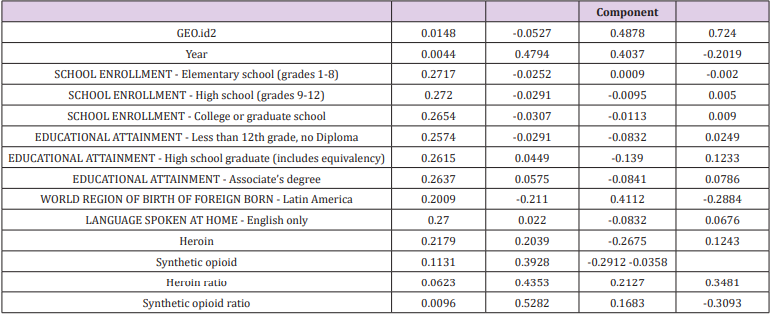
The eigenvector of the principal component is
Among them, uij represents the value of the factor load matrix,
λi represents the eigenvalue, and aij represents the eigenvector.
Therefore, the part of the corresponding feature vector is shown in
Table 7, and the full content is shown in Appendix 5.
Therefore, the main components are:
Among them, akp represents the corresponding feature vector of
the k-th indicator in the i-th principal component, and xp
represents
the p-th index. In the expression of the first principal component,
the coefficients of the 3rd, 5th, 6th, 7th, 8th, 9th, 10th, 11th, 12th, 13th, and
16th indicators are large, and the eleven indicators play a major role,
so we can Think of the first principal component as a comprehensive
indicator consisting of these eleven single indicators. The second,
third and fourth principal components are the same. Any event can
be derived from the opioid flooding score as long as the indicator is
known. For the purposes of this paper, the total score is weighted by
the first four principal components, and the principal component
pre-factors can be the respective variance contribution rates.
which is
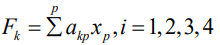
Opioid Class of Abuse Level: According to the principal
component evaluation model based on entropy weight method, the
algebraic value F of the opioid drug flooding score is obtained [6,7].
According to the distribution of F value, the degree of flooding of
opioids is graded, and the filled area map and frequency distribution
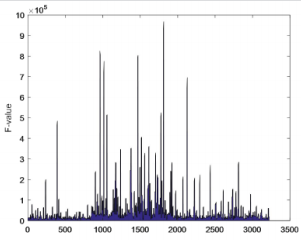
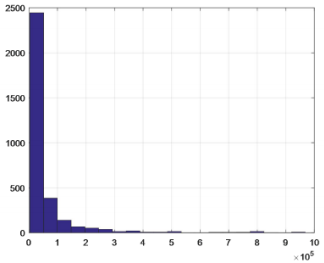
map are obtained. As shown in Figures 8 & 9. It can be seen from
Figures 8 & 9 that the maximum F value is greater than 90,000,
all the data falls within the interval [0, 1000000], and more are
gathered in the interval [0, 450000].In order to effectively classify
the degree of flooding, the interval [0, 400000] is subdivided, and
the data of the degree of flooding between each cell is counted to
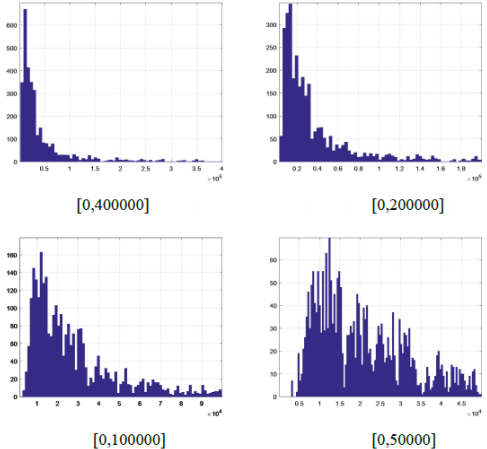
obtain a frequency distribution map, as shown in Figure 10. It can
be found that the comprehensive evaluation value of more than
3000 reports is in the interval [0, 450000], and there are almost
no reports of more than 400,000. Only a few important events can
be seen in Figure 8. For example, the F value of the county 42101 is
96,7854.7 which is the highest, and opioids are the most rampant.
In order to further discover the level of data, the data of this interval
is refined according to the step-by-step refinement analysis method
and is divided into the figures as shown in Figure 10.
From the Figure 10, we can see the obvious hierarchical
distribution. As the interval is continuously refined, it is true that a
large amount of data is found between [0,50000]. As the value of F is
higher, the flood is more serious. Such incidents do occur in practice,
and the use of appropriate opioids occurs in all regions of the United
States, so the number is large. Therefore, according to the frequency
of the degree of opioid influx, the degree of opioid influx is divided
into one to three levels from high to low, see Table 8. The degree of
flooding of opioids in Table 8 is graded, and level 1 indicates the
greatest degree of flooding. In order to verify the rationality of the
classification, combined with the actual considerations, random
or selected boundary values for verification, the data can meet
the requirements and meet the actual facts, which also proves the
rationality and accuracy of the model. At the same time, the F values
of the five counties (39035, 39061, 39113, 42003, 42101) that were
firstly observed were in the serious category, further illustrating
the correctness of the results.
Linear Programming Model
The Foundation of Modexl: In question 1, we have used
system cluster analysis and time series analysis to select the five
counties where opium is the most widespread in the United States.
In question 2, we sorted the weighted composite scores F of 460
counties, and divided 460 counties into three layers according to
the order of F. The larger the value of F, the higher the extent of
opioids in the county. Regarding question 3, we find that if min F
is regarded as an objective function, a linear relationship can be
established between the socio-economic secondary indicators used
and their own primary indicators. That is, all 20 indicators used can
be formed into restrictions. Further, since F1’s contribution rate is
66%, most of the information about the whole can be explained.
Considering the implementation cost of the strategy, in order to
make the effectiveness of the anti-opioid crisis strategy as obvious
as possible, we replace minF with minF1. The linear programming
model is established as follows.
Objective function:
Restrictions
Among them, xk
is the 20 indicators selected by Philadelphia,
and ak
is the corresponding coefficient (parameter).
Model Solution and Sensitivity Analysis: Therefore, we can
use the adjustment of an indicator xk
in the constraint as a strategy
against the opioid crisis. And through the local sensitivity analysis
after the change of xk
, the parameter range (c, k) of each index
is obtained.That is, when the parameter of an indicator is in (c,
k), the optimal solution does not change. It can be preliminarily
understood that when the parameters of an indicator fluctuate in
(c, k), the provided strategy is effective. Of course, we can also bring
the obtained parameter range into the first principal component
score expression to find a new F1 value, and determine whether the
parameter range is valid according to the level of the opioid drug
flood level to which the new F1 value belongs. When the new F1
value is at the third level, the parameter range is successful. When it
is at the second level, the success or failure of the parameter range
is not obvious, that is, the corresponding measures are not effective.
When at the third level, this parameter range is unsuccessful.
Taking the indicator of education as an example, we give
measures to resist the opioid crisis: education is a comprehensive
indicator of importance. Our strategy is to continue to increase
the popularity of basic education in the United States, so that all
people over the age of 25 in the United States will reach at least
the high school education and above. The more a person knows
about the dangers of drugs, the more proficient the correct use of
opioids, the higher the knowledge and personal cultivation, the
less likely he is to take drugs and abuse opioids. Combined with
the above analysis, in the new constraints, the population below
the high school education is 0, and the reduced population is
distributed to the population with higher education. As we analyse
the latest data provided, the data of the five counties of CUYAHOGA,
HAMILTON, MONTGOMERY, ALLEGHENY, and PHILADELPHIA are
substituted into the model. Analyzing the sensitivity of important
coefficients with Lingo and the estimated range of the parameters
can be obtained. Substituting the endpoint value of each parameter
into the first principal component score, the interval of the opioid
flooding scores of the five counties was obtained, and the results
are shown in the following Table 9.
According to Question 2, the grading model of the opioid flooding
scores in the five counties shows that by raising the basic education
level of young people under the age of 25, only Hamilton
County, Ohio (39061) is in the general level of flooding, and the
remaining counties have fallen to lower levels. The level of opioids in
these five counties has dropped from severe to lower or general,
indicating that the future opioid crisis predicted in Part 1 may not
occur. From the overall situation of the five counties, our strategy
is effective.
Strengths
a) In the second problem, the panel data is used in the
dynamic panel data model. Compared with the cross-section data
model, the panel data model controls the deviation of the OLS estimation
caused by the unobservable variables, making the model
more reasonable and the sample estimation of the model parameters more
accurate. Compared with time series data, the panel data
model expands the sample information, reduces the collinearity between
variables, and improves the validity of the estimator. Among
them, the dynamic panel data model can more accurately adjust the
dynamics of the response variables.
b) In question 2, the degree of flooding of opioids was based
on the frequency of F values, and the results were verified.
Weaknesses
a) The data given in question 2 does not take into account
income, economic indicators.
b) In question 2, the degree of spread of opioids is divided
into three layers, with certain subjectivity.
Since some research results are not the focus of answering the
question, and considering the reasons for the paper, the data we
have obtained in the modeling process are not all in the text. However,
some models have good statistical results, so we want to put
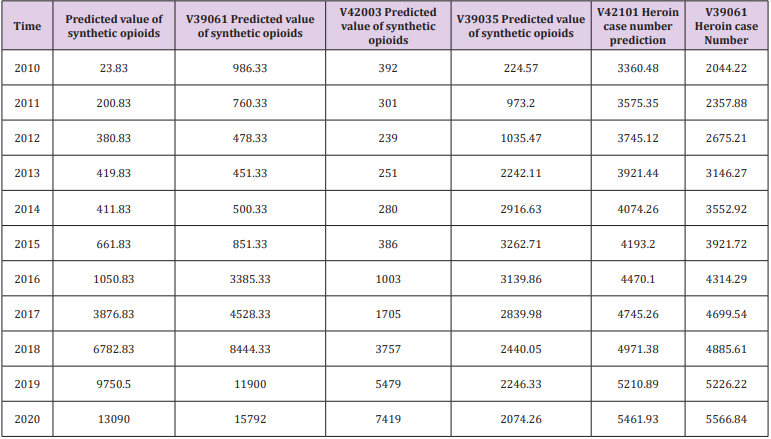
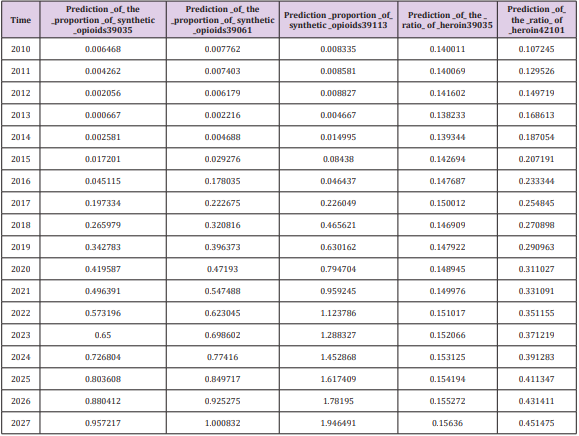
the data passed by the statistical test in the memorandum. The following
Table 10 shows the data prediction results for a time series
analysis during the modeling process. It should be pointed out that
since the known data is only 8 years, we believe that the reliability
of the data in the later years may be verified. The “proportion” in
the Table 11 means the ratio of a given drug to the total number of
drug cases in the county [8]. And our study is limited to the extent
that it focuses on the data provided by NFLIS concerned with opioid
crisis in the US at one time period (2010-2017). After sorting and
analyzing the panel data, we decided to transform the derived data
and then model the panel data, cross-section data and time series
data respectively [9,10]. Next, we consider how to objectively select
a large number of socio-economic data and indicators, and then establish
a model that can reflect two different databases at the same
time, so that the model can be combined with some indicators. Further,
we note that the sample selection strategy may have resulted
in an underrepresentation of heroin users with a prescription opioid
misuse history. Additionally, we note that the findings reported here
may not be completely generalizable to other settings and
time periods [11,12].
We would like to express my gratitude to all those who helped
us during the writing of this article.
More BJSTR Articles: https://biomedres01.blogspot.com
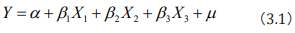
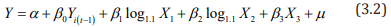
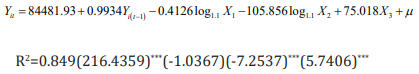
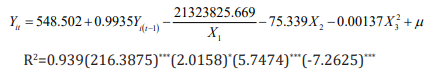
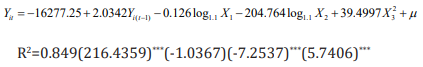
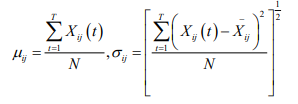
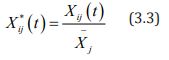
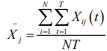 ,after standardization, the mean
value of each indicator is 1, and the variance is
,after standardization, the mean
value of each indicator is 1, and the variance is 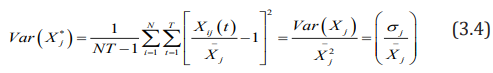
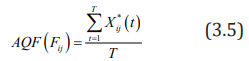 , there are N samples,
each sample records T, and there are p indicators in each period.
, there are N samples,
each sample records T, and there are p indicators in each period.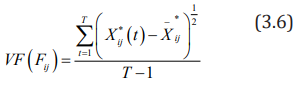
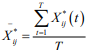
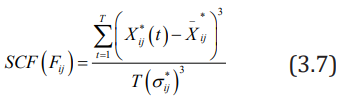 in definition 1, which
reflects the degree of fluctuation of the jth index of sample i over
time.
in definition 1, which
reflects the degree of fluctuation of the jth index of sample i over
time.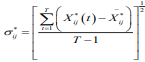 represents the standard deviation of the
jth index of the sample i over the entire period, SCF (Fij) reflects the
degree of symmetry of the jth index of the sample i over the entire
period, SCF F( ij)˂ 0, indicating that most of the index is located to
the right of the average, SCF (Fij)˂ 0, indicating that most of the
indicators are located to the left of the average.
represents the standard deviation of the
jth index of the sample i over the entire period, SCF (Fij) reflects the
degree of symmetry of the jth index of the sample i over the entire
period, SCF F( ij)˂ 0, indicating that most of the index is located to
the right of the average, SCF (Fij)˂ 0, indicating that most of the
indicators are located to the left of the average.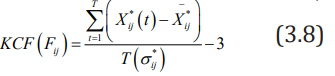


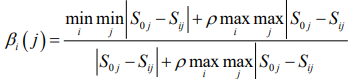
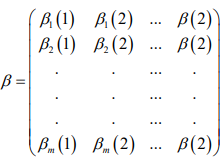
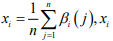 is the degree of association between the i-th
evaluated object and the ideal object. The merits of the object to
be evaluated are evaluated according to the size of the xi
value.
The larger the xi
, the higher the degree of association between the i-th evaluated object
and the ideal object, and thus the better it is
among all the evaluated objects. Because the topic requires judging
whether the use or use trend of opioids is related to the socioeconomic
data of the census, and the part 2 data shows the rules of
the first-level indicators and the second-level indicators, of which
there are 7 first-level indicators. Combining the use and use trends
of opioids (represented by the number of drug cases in each county
and the number of drug cases in each county and the total number
of identified drug cases), the gray correlation analysis is carried out
on 9 indicators. The correlation degree is solved by using MATLAB.
The specific procedure is shown in
is the degree of association between the i-th
evaluated object and the ideal object. The merits of the object to
be evaluated are evaluated according to the size of the xi
value.
The larger the xi
, the higher the degree of association between the i-th evaluated object
and the ideal object, and thus the better it is
among all the evaluated objects. Because the topic requires judging
whether the use or use trend of opioids is related to the socioeconomic
data of the census, and the part 2 data shows the rules of
the first-level indicators and the second-level indicators, of which
there are 7 first-level indicators. Combining the use and use trends
of opioids (represented by the number of drug cases in each county
and the number of drug cases in each county and the total number
of identified drug cases), the gray correlation analysis is carried out
on 9 indicators. The correlation degree is solved by using MATLAB.
The specific procedure is shown in 

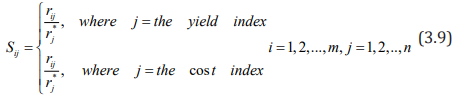
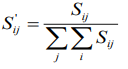
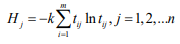 obtained in this way does not destroy the
proportional relationship between the data.
obtained in this way does not destroy the
proportional relationship between the data.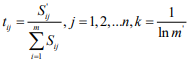
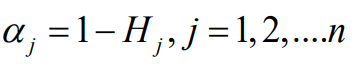 (so the chosen k is such that,
0≤Hj≤1, convenient for subsequent processing)
(so the chosen k is such that,
0≤Hj≤1, convenient for subsequent processing)